Polarisation DC

4.4 PERMITTIVITÉ RELATIVE. RÉGIME PERMANENT

4.4.1 Composition des types de polarisation

Dans la mesure où plusieurs mécanismes de polarisation différents existent simultanément, leurs effets s'additionnent. En caractérisant par un indice i les nombres volumiques de porteurs de moments dipolaires, les facteurs de polarisation et les champs locaux propres à chacun de ces mécanismes, la polarisation globale s'obtient par une généralisation de (4.37) de la forme :

 

               (4.53)

Si le diélectrique peur être considéré comme isotrope, ou s'il présente une symétrie cubique comme celle qui découle de la figure 4.8, le calcul du champ local développé au paragraphe 4.3.1 s'applique. Il en découle que E_L a la même valeur pour tous les types de dipôles, donc

                     (4.54)

Il est maintenant possible d'exprimer la permittivité relative en fonction des facteurs de polarisation. En portant (4.35) dans (4.54) il vient :

                                   (4.55)

En identifiant cette expression de la polarisation à celle donnée par (4.25), on tire pour ε_r  l'expression :

                    (4.56)

connue sous le nom d'équation de Clausius-Mosotti. Cette équation relie les propriétés microscopiques α_i à la grandeur macroscopique qu'est la permittivité.

4.4.2  Remarque

On pourrait s'attendre à ce que plusieurs mécanismes de polarisation interagissent entre eux. Dans la grande majorité des diélectriques ce n'est pas le cas, une variation linéaire de la polarisation en fonction du champ appliqué en fournit la preuve. Une telle interaction existe par contre dans les matériaux ferroélectriques.

4.4.3  Permittivité d'un mélange homogène

Les diélectriques utilisés en pratique se présentent souvent sous la forme de mélanges. On peut ainsi varier certains paramètres et obtenir une combinaison optimum de propriétés correspondant à une application donnée.
Par exemple, dans les liquides, on modifie de cette façon la viscosité, le point de solidification, la permittivité etc... Dans les thermoplastiques, l'adjonction de diverses substances permet d'améliorer la stabilité chimique, d'abaisser le prix volumique, d'augmenter la résistance mécanique, etc....
L'utilité d'une formule donnant la permittivité d'un mélange est donc évidente. Si le mélange est parfaitement homogène, la relation (4.56) est utilisable sous la forme :

           (4.57)

où ε_m est la permittivité relative du mélange, ε_i celle du constituant No i. Il y a n constituant occupant chacun une fraction Y_i du volume total.
Dans de nombreux cas, le mélange ne peut pas être considéré comme homogène à l'échelle microscopique. Alors, il n'existe pas de théorie absolument rigoureuse permettant d'obtenir une formule valable d'une façon générale. Plusieurs formules approchées ont été établies sur des bases théoriques, empiriques ou les deux à la fois.

4.4.4 Permittivité d'un mélange sous forme de dispersion

Une formule approchée peut être obtenue théoriquement, dans ce cas. Pour l'établir, on part d'un premier diélectrique (indice 1), appelé diélectrique hôte, initialement pur et possédant une permittivité relative ε₁. L'effet dans ce diélectrique d'une inclusion sphérique du diélectrique additionnel (indice 2), de permittivité relative ε₂ est tout d'abord évalué, en termes de perturbation du potentiel (fig. 4.16). Le mélange des diélectriques étant considéré par la suite comme une dispersion de petites sphères du diélectrique additionnel dans le diélectrique hôte, on obtient la permittivité du mélange en sommant l'effet de toutes ces sphères.

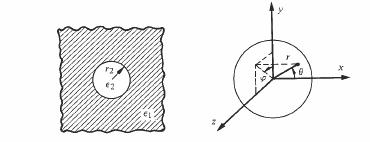
Fig. 4.16 Inclusion dans le diélectrique hôte et référentiel utilisé pour calculer le potentiel.

Le potentiel V dans les milieux 1 et 2 est régi par l'équation de Poisson :

             (4.58)

On peut admettre sans autres que la densité de charges libres p_q dans le diélectrique est assez faible pour être négligée. Soit E_o le champ électrique homogène, orienté selon x, régnant dans le diélectrique hôte pur. Après l'introduction de la sphère, le potentiel présente une symétrie de révolution autour de l'axe x. L'équation (4.58) prend donc la forme :

           (4.59)

valable dans les deux milieux. La solution générale de (4.59) s'écrit :

    (4.60)

où les A_n et B_n sont des ensembles de constantes déterminées par les conditions de continuité imposées à l'interface des milieux 1 et 2, P_n désignant le polynôme de Legendre d'ordre n. L'équation (4.60) est valable pour une inclusion de forme quelconque, mais admettant une symétrie de révolution autour de x. Dans le cas d'une inclusion sphérique, seuls les termes correspondant à n = 0 et n=1 subsistent. On peut donc écrire (4.60), à une constante additive près sans importance puisqu'il s'agit d'un potentiel, sous la forme :

     (4.61)

L'indice i valant 1 ou 2 selon le milieu considéré. Les quatre constantes d'intégration sont déterminées par les conditions suivantes:

•  •  V₂ est fini en r= 0, ce qui entraîne B₂ = 0        (4.62)


•  •  la composante tangentielle de E est continue à la surface de la sphère:

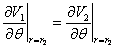                     (4.63)

  
  
•  •  la composante normale de D est continue à la surface de la sphère:
  

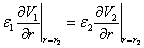            (4.64)

  
  
•  •  à l'infini, E n'est plus perturbé par la présence de l'inclusion et vaut E_o,

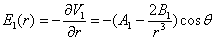                     (4.65)

 En posant R = infini et θ = 0 il vient :

 

A₁ = - E_o                    (4.66)

En exprimant (4.63) et (4.64) un moyen de (4.61), on obtient finalement :

 

                      (4.67)

et

                             (4.68)

 

On remarque que V₂ ne dépend que de r cos θ, c'est-à-dire de x. Dans les inclusions, les équipotentielles sont donc les plans perpendiculaires à x. Il s'ensuit que E₂ a la même valeur en tout point de l'inclusion (fg. 4.17).

 

            (4.69)

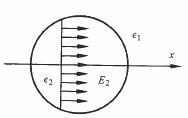
Fig. 4.17 Champ électrique dans l'inclusion

Lorsque ε₁ > ε₂, le champ dans l'inclusion est plus élevé que dans le diélectrique hôte. Ce résultat a son importance dans le cas de diélectriques présentant des inhomogénéités telles que des bulles.

Soient maintenant N inclusions réparties uniformément à l'intérieur d'une sphère S de rayon R >> r₂, toujours située dans le diélectrique hôte (fig. 4.18).

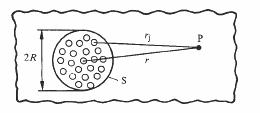
Fig 4.18

Si la densité des inclusions dans S n'est pas trop grande, on peut exprimer leur contribution au potentiel en P, V_NP, par la somme des contributions de chaque inclusion prise séparément. La contribution d'une inclusion est donnée par le deuxième terme de (4.67), on a donc :

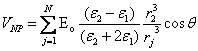             (4.70)

expression que l'on peut simplifiera condition de placer P suffisamment loin de S pour que R soit petit vis-à-vis de r. Alors

                   (4.71)

En considérant S comme faite d'un diélectrique homogène de permittivité relative inconnue e_m, la contribution de cette sphère au potentiel en P s'écrit :

                  (4.72)

d'où ε_m, par identification de (4.71) et (4.72)

                 (4.73)

En appelant Y = Nr₂³/R³ la fraction en volume du diélectrique additionnel, il vient :

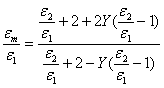         (4.74)

C'est la formule recherchée. Les résultats qu'elle fournit sont d'autant meilleurs que la dispersion est moins dense ou que les permittivités des milieux 1 et 2 sont voisines, car c'est dans ces conditions que la superposition des effets (4.70) est la mieux vérifiée.

4.4.5 Permittivité d'un polymère expansé

Dans les polymères expansés l'expérience montre qu'une relation logarithmique du type

                   (4.75)

donne des résultats satisfaisants. Si ε_r est la permittivité du diélectrique homogène et d sa densité, alors que d' est la densité du matériau expansé, (4.75) s'écrit simplement :

            (4.76)

La figure 4.19 montre la variation de permittivité du polystyrène expansé

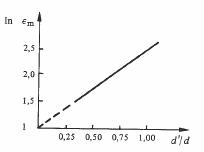
Fig. 4.19