Dielectrique

PROPRIÉTÉS DIÉLECTRIQUES

4.1  INTRODUCTION, GÉNÉRALITÉS

Selon le modèle des bandes d'énergie (sect. 2.6) la matière devient diélectrique, c'est à dire mauvaise conductrice de l'électricité, quand les bandes de conduction et de valence sont séparées par une énergie supérieure à 5 eV. Alors, un très petit nombre seulement d'électrons reçoivent, à température ordinaire, l'énergie thermique nécessaire pour effectuer une transition dans la bande de conduction. Quand la température s'élève la probabilité de transition augmente, et l'on observe pour la conductivité σ une dépendance du type :

σ = σ_o exp (-W/k_BT)                                                     (4.1)

W est interprété comme une énergie d'activation du processus de conduction. La relation (4.1) est valable dans les diélectriques cristallins et amorphes, ainsi que les diélectriques partiellement cristallins tels que les polymères.

Schématiquement, on peut considérer les diélectriques comme des substances dans lesquelles tous les électrons sont si fortement liés à leur(s) atome(s) qu'ils ne peuvent être responsables d'un courant électrique. Dans ces conditions, un courant d'origine ionique est également exclu.

Le fait que les charges présentes dans un diélectrique ne soient pas libres ne signifie nullement qu'elles sont liées de façon absolument rigide les unes aux autres. En particulier, un champ électrique appliqué E déplace légèrement les charges positives et négatives les unes par rapport aux autres, provoquant l'apparition de dipôles électriques. Plusieurs mécanismes différents concourent à l'apparition de ces dipôles ( 4.3.3). Si E varie au cours du temps, sinusodalement par exemple, on observe à partir de certaines fréquences, un déphasage entre ce champ et l'établissement des dipôles (sect. 4.5). Ce déphasage provoque la dissipation d'énergie responsable des pertes diélectriques. Enfin, si le champ électrique ou la température dépassent certaines valeurs, une conduction électrique peut se développer de façon brutale, détruisant le diélectrique localement ou dans sa totalité (sect. 4.7).
La conductivité σ, la permittivité ε, les pertes en régime variable tan δ, le champ électrique maximum admissible E_c sont les quatre grandeurs au moyen desquelles l'ingénieur électricien caractérise le plus souvent un diélectrique. La permittivité et une partie des pertes diélectriques sont liées directement au processus de polarisation (apparition des dipôles). La conductivité et le champ maximum admissible dépendent fortement de la pureté et de la structure des matériaux. L'étude de ces deux grandeurs est essentiellement expérimentale (sect. 4.7). Quelques propriétés spéciales comme la piézoélectricité et la ferroélectricité sont abordées à la section 4.9.
Diélectrique et isolant sont en principe synonymes, bien qu'on parle plus volontiers d'isolant quand les valeurs de σ et E_c sont les plus importantes, et de diélectrique quand ce sont celles de ε et tan δ. Par exemple on dit l'isolant d'un câble et le diélectrique d'un condensateur.
Certains isolants développés et utilisés dès le siècle dernier ont des propriétés remarquables et sont encore employés actuellement comme le papier, l'huile minérale, le verre, etc. L'industrie des polymères et de récents développements dans le domaine des céramiques marquent aujourd'hui très fortement le marché des isolants. Les matériaux industriels les plus importants sont décrits aux sections 4.10 à 4.14.

4.2 LOIS MACROSCOPIQUES, DÉFINITIONS

4.2.1 Electrostatique dans le vide. Rappel

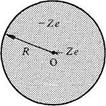
Deux charges électriques ponctuelles q₁ et q₂ séparées par une distance r₁₂ (fig.4.1) exercent l'une sur l'autre des forces F₁ et F₂ données par la loi de Coulomb:

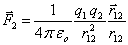                          (4.2)

où ε_o est la permittivité du vide et vaut 8,85 10^-12 F/m.




Fig. 4.1  Cas où q₁ et q₂ sont de même signe.

Un ensemble de charges q_i crée dans l'espace un champ de déplacement D défini par :     

                                (4.3)

Dans cette expression dA = n dA, dA étant un élément de la surface fermée A contenant les charges q_i (fig. 4.2); n est un vecteur unité perpendiculaire à A et dirigé vers l'extérieur. L'intégrale porte sur toute la surface. On reconnaît en (4.3) l'expression du théorème de Gauss.

Si A est une sphère de rayon r, et si le système de charges se réduit à une charge


Surface A
                        Fig. 4.2


ponctuelle unique q placée au centre de A, (4.3) donne pour valeur de D sur la sphère :

                                                                              (4.4)

Dans le cas où A contient une densité volumique de charges ρ l'équation (4.3) s'écrit : 



                            (4.5) 

où V est le volume délimité par A. Le théorème de la divergence permet d'exprimer (4.5) sous la forme:


div D = ρ                      (4.6)

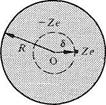
L'effet d'un ensemble de charges peut non seulement être mesuré par D, mais encore par le champ électrique E. Il existe en un point P de l'espace un champ E lorsqu'une charge q placée en P y subit une force F donnée par :


F = q E                                                 (4.7)

Les champs E et D sont deux mesures différentes d'une même propriété de l'espace créée par la présence de charges électriques. Il doit donc exister une équation liant ces deux grandeurs. On l'établit facilement en étudiant le système de la figure 4.3




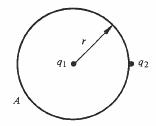
Fig. 4.3


La charge q₂ est infiniment proche de la sphère, mais à l'extérieur de celle-ci, q₁ est au centre. Les équations (4.2), (4.4) et (4.7) permettent d'écrire :

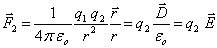                                   (4.8)

Dans le vide le champ de déplacement et le champ électrique sont donc liés par la relation:

D = ε_o E                                                                        (4.9)

Ces deux grandeurs jouent des rôles totalement comparables, une seule d'entre elles serait suffisante pour décrire les phénomènes. Il n'en sera plus ainsi à l'intérieur de la matière ( 4.2.6).

4.2.2 Moment dipolaire

Un dipôle électrique ( III 3.3.3) est un système formé de deux charges ponctuelles de même valeur mais de signe opposés, séparées par une distance d (fig. 4.4).

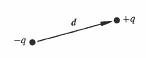
Fig. 4.4 Dipôle électrique (modèle).


L'importance de ce dipôle est mesurée par son moment dipolaire p défini par:


p = q d                              (4.10)

Si d -> 0 alors que p reste constant on obtient, à la limite, un dipôle ponctuel.

Les diélectriques recèlent divers types de dipôles décrits au paragraphe 4.3.3. Aucun d'entre eux ne se présente exactement comme celui de la figure 4.4, mais ce dernier peut servir de modèle pour chacun des types rencontrés.

4.2.3 Vecteur polarisation P

Soit un volume V, limité par la surface fermée A, et contenant N dipôles. La charge globale de V est nulle. Si l'orientation des dipôles est parfaitement aléatoire, V ne présente pas, à l'échelle macroscopique, de propriété particulière. Si par contre l'orientation des dipôles n'est pas aléatoire, V présentera un moment dipolaire macroscopique P_V.

                                                                              (4.11)

Dans un volume d V, en principe infinitésimal mais supposé tout de même assez grand pour contenir un nombre élevé de dipôles, on peut définir une densité de moment dipolaire P, faisant ainsi le passage d'un ensemble de  dipôles discrets à une distribution continue de moment dipolaire. Si dp est la somme vectorielle des moments dipolaires contenus dans d V,

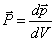                                                                 (4.12)

On appelle aussi P, vecteur polarisation ou simplement polarisation. A l'échelle du volume V, dans le modèle continu, l'équation (4.11) s'écrit :



                                                            (4.13)

4.2.4 Représentation d'un état de polarisation

On peut montrer [52] que le potentiel créé par les moments dipolaires contenus dans V est identique à celui créé par une densité volumique ρ' de charges réparties dans V, complétée par une densité superficielle σ' de charges réparties sur A, et telles que :

σ' = P n                                                         (4.14)


ρ'  = - div P                                                 (4.15)


où n est encore le vecteur unité normal à A et dirigé vers l'extérieur. Les primes sont là pour indiquer que ces distributions de charges sont fictives. Seuls les dipôles contenus dans V ont une réalité physique. L'intérêt de (4.14) et (4.15) réside en ceci qu'il est toujours possible de remplacer dans l'étude d'un système comprenant un milieu polarisé électriquement, l'effet des moments dipolaires par celui de σ' et ρ'. Il en résulte une simplification des calculs et une meilleure compréhension des phénomènes. La charge globale de V étant nulle,


                                                               (4.16)


Dans le cas le plus fréquent où div P = 0, seule la charge superficielle subsiste (fig.4.5).




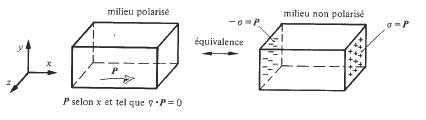
Fig. 4.5

4.2.5 Charges réalisées. Définition

Dans le cas général, un diélectrique peut contenir, en plus des dipôles dont l'effet peut être décrit par σ' et ρ', des densités de charges superficielles et en volume, σ et vρ correspondant à la présence de charges réelles.

On appelle ces dernières charges réalisées [53] pour les distinguer des charges virtuelles correspondant à σ' et ρ'.

4.2.6 Champ électrique et champ de déplacement à l'intérieur d'un diélectrique

On pourrait définir D et E à l'intérieur d'un diélectrique de la même manière que dans le vide, car un diélectrique peut être considéré comme un assemblage de dipôles et charges ponctuelles placés dans le vide. Soient D_m et D_m le déplacement et le champ qui résulteraient de cette procédure. L'équation (4.6) prendrait la forme :


div D_m = ρ + ρ'                                                                    (4.17)


L'équation liant E_m à D_m aurait la même forme que (4.9) :

D_m = ε_o E_m                                                      (4.18)

A l'intérieur de la matière, comme dans le vide, les rôles du champ de déplacement et du champ électrique seraient totalement comparables. Une seule de ces grandeurs serait donc suffisante.

Mais, par convention, le champ de déplacement dans un diélectrique n'est dû qu'aux charges réalisées. Le champ D_m tel qu'il est défini par (4.17) n'est pas utilisé en électricité. L'équation (4.9) ne prend donc pas, dans la matière, la forme (4.18). On a :


div D = σ = div D_m - ρ'                                                           (4.19)

Par (4.15), à une constante additive près, choisie égale à zéro, il vient:

D = D_m + P                                                                         (4.20)
Par convention toujours, le champ électrique à l'intérieur d'un diélectrique résulte de la présence de la polarisation et de celle des charges réalisées. Par conséquent,

E = E_m                                                                            (4.21)

d'où par (4.18) et (4.20),

D = ε_o E + P                                                                          (4.22)

4.2.7 Susceptibilité diélectrique. Définition

Dans les diélectriques (ferroélectriques exceptés), la polarisation est provoquée par le champ électrique et disparaît avec lui. Il est donc naturel de poser :

P= χ_r ε_o E                                         (4.23)


On appelle χ_r la susceptibilité diélectrique relative. C'est une grandeur sans dimensions. Lorsque χ_r est indépendant de E, on a à faire à un diélectrique linéaire.

4.2.8  Permittivité. Définitions

La forme de (4.23) suggère de contracter les deux termes du second membre de (4.22). On écrit:

D = ε_oε_r E                                                        (4.24)


On appelle ε_r la permittivité relative du diélectrique. Le produit ε_o ε_r, noté souvent simplement ε, est appelé permittivité absolue du diélectrique. En éliminant D de (4.22) et (4.24) il vient:

P = ε_o (ε_r - 1) E                                                             (4.25)

donc

χ_r = ε_r - 1                                                                           (4.26)

4.3 POLARISATION À L'ÉCHELLE MICROSCOPIQUE

4.3.1 Champ local E_L

Dans un milieu polarisé, le champ électrique varie sur la distance séparant un dipôle de son voisin. Cette variation à l'échelle microscopique n'est pas décrite par les équations de Maxwell, qui ne relient entre elles que des grandeurs représentatives à l'échelle macroscopique. Ces grandeurs sont des mesures moyennes des phénomènes se déroulant à l'échelle des atomes.

Pour calculer la contribution d'un dipôle à la polarisation P en fonction de données microscopiques, il est indispensable de connaître le champ électrique local E_L agissant directement sur ce dipôle. Ce champ peut être calculé en fonction de E et P.
Sans restreindre la généralité du résultat, on établira l'expression de E_L dans le cas d'un champ électrique homogène tel qu'il existe dans un condensateur plan (fig. 4.6 (a)).


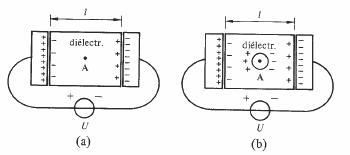
Fig. 4.6  L'effet de P est remplacé par les charges représentées schématiquement dans le diélectrique.


Le champ local au point A comprend deux composantes :

E_L = E + E_dip                                                        (4.27)


où E est le champ imposé par la source de tension U. Ce champ ne dépend pas de la présence du diélectrique entre les armatures du condensateur, il est égal à U/l; E_dip est le champ résultant de la présence de dipôles dans tout le volume du diélectrique.

On calcule facilement E_dip par la procédure suivante, due à Lorentz. Le diélectrique est formellement divisé en deux régions par une sphère S centrée en A (fig. 6 (b)). A l'intérieur de S, l'effet de chaque dipôle est pris en compte individuellement, en considérant tout d'abord les plus proches voisins de A, puis les deuxièmes plus proches voisins, et ainsi de suite jusqu'aux voisins situés sur S. Le rayon de la sphère est suffisant pour qu'à l'extérieur de S, la distance des dipôles au point A soit très grande par rapport à la distance séparant deux dipôles voisins. L'effet en A des dipôles extérieurs à S peut donc être remplacé par celui d'une distribution continue de moment dipolaire. On pose par conséquent :

E_dip = E_i + E_e                                                       (4.28)


où E_i et E_e sont les champs créés par les dipôles situés respectivement à l'intérieur et à l'extérieur de S. Le champ E (fig. 4.7) produit par un dipôle ponctuel p s'exprime en coordonnées polaires ( 4.16.1) par:

                                                  (4.29)

et




                                                   (4.30)




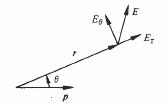
Fig. 4.7


Dans un cristal où les voisins de A sont disposés selon la figure 4.8 (réseau cubique), on déduit des équations (4.29) et (4.30) que E_i = 0.




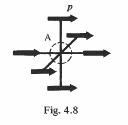
Fig. 4.8

L'effet des dipôles extérieurs à S peut être remplacé par une distribution superficielle de charges σ'(θ) située sur S (fig. 4.9).




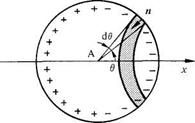
Fig. 4.9 E et P sont portés par x.


Selon (4.14) la charge d σ' portée par le segment élémentaire de la figure 4.9 vaut

d σ' = - P cos θ 2π r² sin θ  dθ                         (4.31)


La force élémentaire dF due à dσ' agissant sur une charge positive q placée en A est, par raison de symétrie, portée par x. En comptant dF positivement dans le sens de xon a, par la loi de Coulomb,

dF = q dσ' cos θ / 4πε_or²                                                       (4.32)


d'où la force totale, sur q:


 F =    - P q cos³θ / 6ε_o intégré entre 0 et π                                         (4.33)

Le champ créé en A par les dipôles extérieurs à S vaut donc


E_e = P / 3ε_o                                                    (4.34)

Finalement, le champ local agissant sur un dipôle est donné par l'expression

E_L = E + P / 3 ε_o                                                 (4.35)

D'autres approximations du champ local ( 4.16.2) ne font pas appel à l'hypothèse d'un réseau cubique.

4.3.2 Facteur de polarisation α. Définition

Soit p le moment dipolaire d'un atome ou d'une molécule, projeté sur le champ local E_L auquel cet atome ou cette molécule est soumis. On appelle facteur de polarisation α le rapport
α = p  / E_L                            F/m²                                           (4.36)


Si N est le nombre volumique des porteurs de p, la polarisation due à ces derniers vaut

P = N α E_L                                            (4.37)

4.3.3 Mécanismes de polarisation

Les plus importants mécanismes concourant à l'apparition de p sont représentés schématiquement dans le tableau 4.10 :

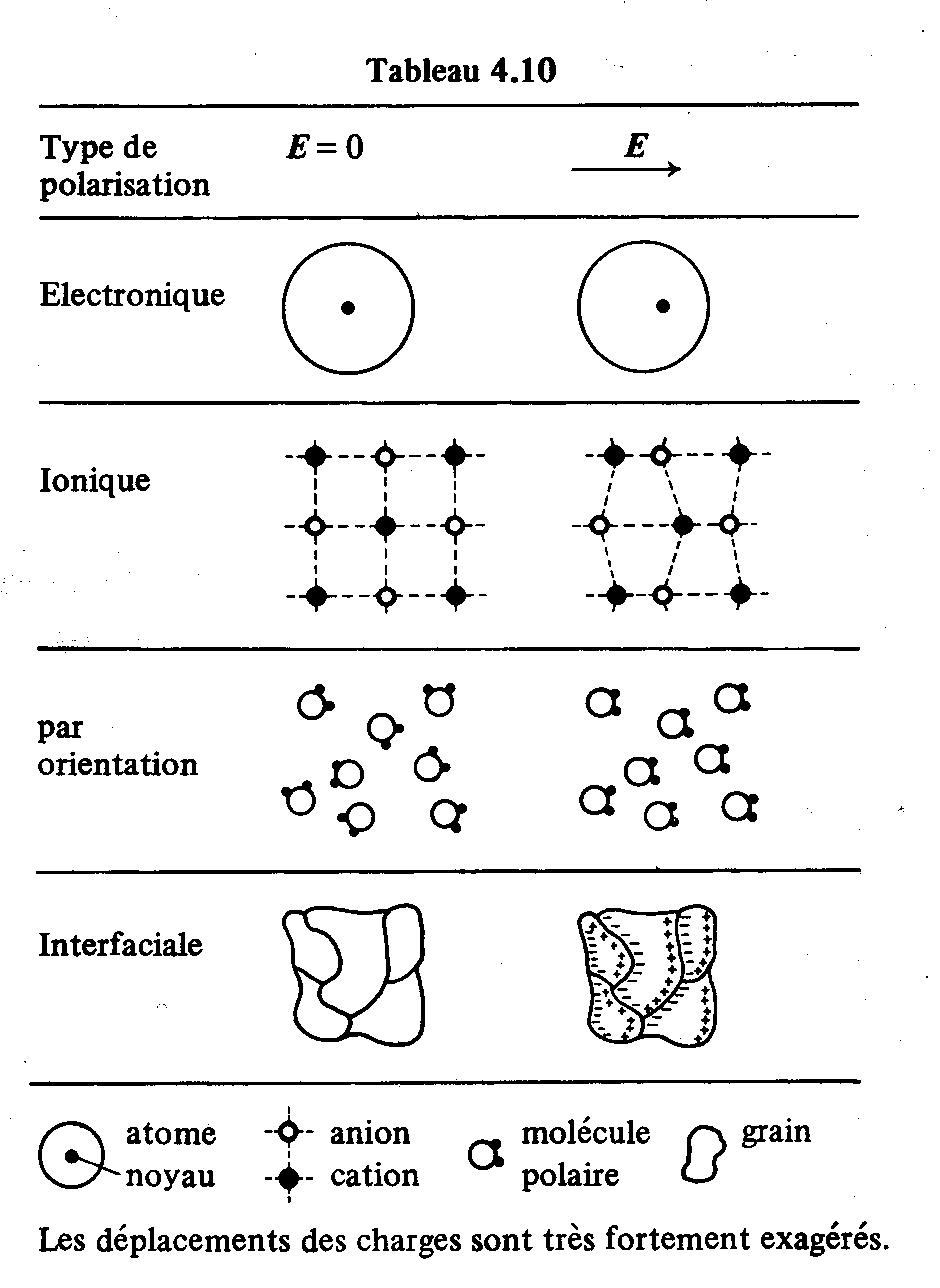
• La polarisation électronique est due à un déplacement relatif du noyau de l'atome par rapport à l'ensemble des électrons qui l'entourent. Tous les atomes présentent, à des degrés divers, ce type de polarisation qui s'établit en un temps très court, et reste sensible jusqu'à des fréquences dépassant celles de la lumière visible (1015 Hz). C'est pourquoi la polarisation électronique est appelée souvent polarisation optique.
  
• La polarisation ionique ne se rencontre que dans les cristaux ioniques. Elle résulte du déplacement en sens contraires des ions de signes opposés. Cette polarisation s'établit plus lentement que la précédente, elle se manifeste jusqu'à des fréquences comprises entre les hyperfréquences et l'infrarouge.
  
• Le plus souvent, une molécule formée d'atomes différents possède un moment dipolaire spontané, c'est-à-dire indépendant de l'existence d'un champ extérieur. En l'absence d'un tel champ, ces moments sont orientés de façon aléatoire, de sorte qu'il n'y a pas de polarisation macroscopique observable. Sous l'effet d'un champ, par contre, les moments ont tendance à s'aligner. Il en résulte une polarisation appelée polarisation par orientation, se manifestant jusqu'à des fréquences comprises entre 1 kHz et 1 MHz. En plus de ce phénomène d'orientation, le champ peut faire varier le moment de la molécule, par déformation de cette dernière et de ses orbitales.
• Les porteurs de charges, jamais totalement absents dans un diélectrique, migrent sous l'effet du champ et ont tendance à se concentrer autour de défauts tels que les impuretés, les lacunes, les joints de grains, etc. On regroupe sous le nom de polarisation interfaciale, la polarisation résultant des accumulations locales de charges dues à l'ensemble des phénomènes de migration. Cette polarisation est caractérisée par le temps d'établissement le plus long de tous : il peut atteindre plusieurs minutes et même davantage.

Les polarisations électronique, ionique et par orientation font l'objet de modèles d'une portée générale, dont les plus simples sont étudiés dans les paragraphes suivants. La diversité des mécanismes à l'origine de la polarisation interfaciale ne permet pas d'en obtenir un modèle général. On ne cherchera donc pas à expliciter le facteur de polarisation interfaciale α_if.
Le sujet de la polarisation électrique est traité de manière fondamentale dans [54].
La fin de cette section est consacrée à la polarisation sous champ électrique constant. La section suivante aborde la polarisation sous champ sinusodal.

4.3.4 Polarisation électronique

La polarisation électronique peut être décrite par le modèle classique suivant. L'atome est considéré comme formé d'un noyau ponctuel, portant une charge Ze. Ce noyau est entouré d'électrons confinés dans une sphère de rayon R, à l'intérieur de laquelle ils produisent une densité de charges p uniforme. En l'absence de champ, le noyau se trouve au centre O de la sphère (fig. 4.11). 

E = 0	EL

                       Fig. 4.11


Un champ local E_L crée des forces F_r tendant à extraire le noyau de la sphère chargée. Mais un déplacement δ du noyau par rapport à O crée à son tour des forces d'attraction coulombienne F_a tendant à ramener le noyau en O. Le déplacement du noyau est donc déterminé par la condition d'équilibre F_a= F_r. On a

F_r = Z e E_L                                                        (4.38)

Supposons que la sphère contenant les électrons ne se déforme pas sous l'action de E_L. Selon le théorème de Gauss, seule la charge électronique contenue dans la sphère de rayon S produit une force attractive sur le noyau. Par (4.5) le champ de déplacement dû à cette charge, à la surface de la sphère, vaut :

D(δ)= -Z e δ/4πR³                                      (4.39)

d'où

F_a = -(Z e)²δ / 4π ε_o R³                                                    (4.40)


La condition d'équilibre devient

Ze = 4 πε_oR³E_L = p                                                                (4.41)

où p représente le moment dipolaire de l'atome. On déduit immédiatement de (4.41) le facteur de polarisation électronique α_el:


α_el = 4 π ε_oR³                                                                                (4.42)

II est intéressant de constater que α_el ne dépend pas du nombre atomique, mais seulement de R, qui représente en fait le rayon de l'atome. Malgré l'extrême simplicité du modèle, (4.42) donne pour ε_el des ordres de grandeur corrects, en particulier dans le cas des gaz rares dont la structure électronique est la plus proche des hypothèses de départ.

La structure électronique des atomes variant peu avec la température, on doit s'attendre qu'il en soit de même pour la polarisation électronique. Ce fait est confirmé par l'expérience.

4.3.5 Polarisation ionique

Considérons le cas d'un monocristal ionique de structure cubique simple, dont la direction < 100> est parallèle au champ appliqué, et au champ local qui en résulte.


Sous l'action de E_L les ions se déplacent (fig. 4.12) d'une quantité Δx par rapport à leurs positions de repos.





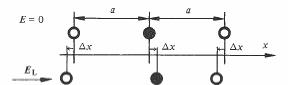
Fig. 4.12 , cation (ion de référence) ; , anion ; a, distance des ions en position de repos (E =0).


Δx correspond à l'équilibre entre les forces de rappel (valence) et la force due au champ local. Pour les petits déplacements dont il est question ici, les forces de rappel peuvent être supposées proportionnelles à Δx. En ne considérant que l'un des deux voisins de l'ion de référence, la force de rappel vaut :

F_r = 2 γ Δx                                            (4.43)


La constante de rappel γ se déduit de l'énergie de liaison W(x) de ces deux ions. Par (1.36)


γ = 1/2 ∂² W / ∂x² en x = a                                          (4.44)



En tenant compte des deux voisins de l'ion de référence, l'équilibre des forces s'écrit

4 γ  Δx = n e E_L                                                               (4.45)


où n est le nombre de charges électroniques porté par les ions.

Le moment dipolaire résultant des déplacements x des ions de la figure 4.12 vaut:

 p = ne (a + 2 x) - ne (a - 2 x) = 4 ne Δx               (4.46)


d'où

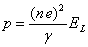                                                          (4.47)
 Le facteur de polarisation ionique α_io est donc égal à


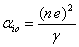                                                                   (4.48)


L'énergie W(x) étant pratiquement indépendante de la température (changements de phases réservés), il en est de même du facteur de polarisation ionique.

4.3.6 Polarisation par orientation

Pour que deux atomes différents A et B forment une molécule, il est nécessaire que l'un d'entre eux ait une tendance plus marquée à partager un ou plusieurs de ses électrons avec l'autre. Supposons que c'est A qui présente cette tendance. On dit que A est électropositif et B électronégatif. Le transfert de charges de A vers B ne porte pas nécessairement sur un nombre entier de charges électroniques. Il se peut que l'électron fourni par A ne passe qu'une partie de son temps au voisinage de B et qu'il reste, le complément du temps, au voisinage de A (covalence). Dans tous les cas, puisqu'il n'y a pas de transfert de charges au niveau des noyaux, la molécule présente un moment dipolaire spontané p_m.

Dans une molécule comprenant plus de deux atomes, plusieurs liens peuvent présenter un moment dipolaire spontané. Le moment dipolaire de la molécule est alors égal à la somme vectorielle de ceux-ci. La figure 4.13 représente deux configurations possibles d'une molécule hypothétique A₂B. La figure 4.13 (a) correspond à la molécule CO₂ qui, parfaitement symétrique ne présente cas de moment dipolaire spontané. La figure 4.13 (b) à celui de H₂O qui, avec un angle A-B-A de 104 présente un moment dipolaire p_m = 6.1 10^-30 C m.



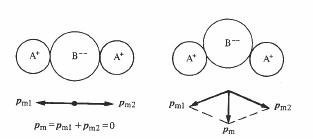
(a)                                (b)

Fig. 4.13

Une molécule dont la formule chimique est symétrique peut ne pas être polaire. C'est le seul renseignement de nature électrique fourni par la formule elle-même (fig. 4.14).




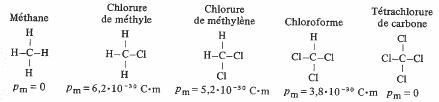
Fig. 4.14


II est évident que seuls le méthane et le tétrachlorure de carbone peuvent n'être pas polaires, et en réalité ils ne le sont pas. L'atome de chlore étant plus gros que celui d'hydrogène, on doit s'attendre à ce que le moment dipolaire spontané des autres molécules soit le plus élevé pour CH₃C1 et le plus faible pour CHCl₃, ce fait est confirmé par l'expérience.

Les deux polymères dont les molécules linéaires sont représentées à la figure 4.15 sont des diélectriques très utilisés. La forme de la molécule de polyéthylène n'est pas aussi simple que le laisserait supposer sa formule chimique. Toutefois, la symétrie est parfaite et le polyéthylène non polaire.
La formule du polychlorure de vinyle (PVC) ressemble à celle du polyéthylène,




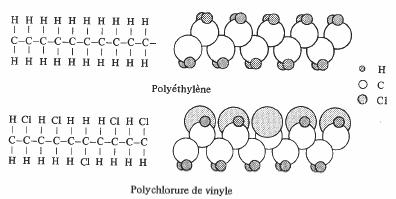
Fig 4.15


à ceci près qu'un atome de carbone sur deux voit l'un de ses atomes H remplacé par un atome Cl. La substitution porte sur l'un ou l'autre des liens de valence concernés, ce qui donne un certain caractère aléatoire à la molécule de PVC. Ceci ne l'empêche pas de rester franchement asymétrique, et de présenter par conséquent un moment dipolaire assez important.

Soumis à un champ local E_L avec lequel il fait un angle γ, un moment dipolaire p_m subit un couple C:


C = P_m X E_L                                                                              (4.49)

tendant à aligner ce dipôle sur E_L.
L'énergie potentielle du dipôle dans le champ électrique local est donnée par:

W_pot = - p_m E_L

L'énergie potentielle électrique est minimum lorsque le dipôle est aligné avec le champ électrique.
Un ensemble de dipôles électriques identiques est réparti en énergie selon une distribution statistique de Boltzmann.

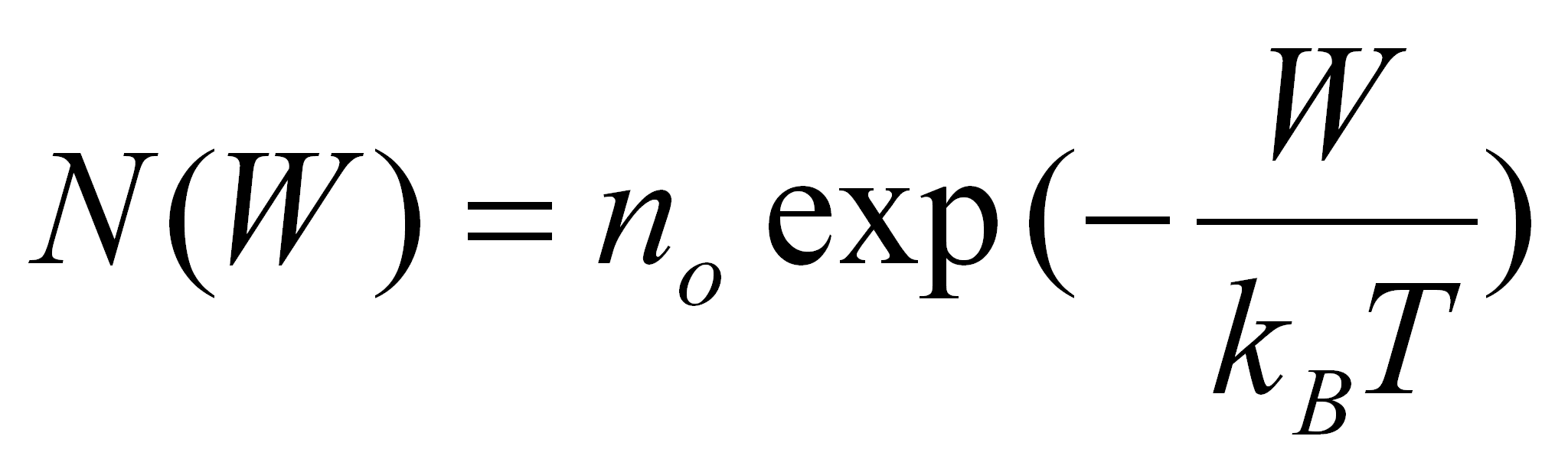                                                              (4.49b)

Beaucoup de dipôles sont alignés avec le champ électrique, peu lui sont opposés. n_o est déterminé par l'intégrale de la fonction de Boltzmann sur tout l'espace des énergies, qui doit être égale à la densité volumique de dipôles.
La polarisation moyenne P est calculée en intégrant les projections des dipôles sur les 3 axes d'un repère cartésien x, y et z. En choisissant arbitrairement de mettre l'axe z selon le champ électrique, il vient par exemple pour la projection selon z, que:
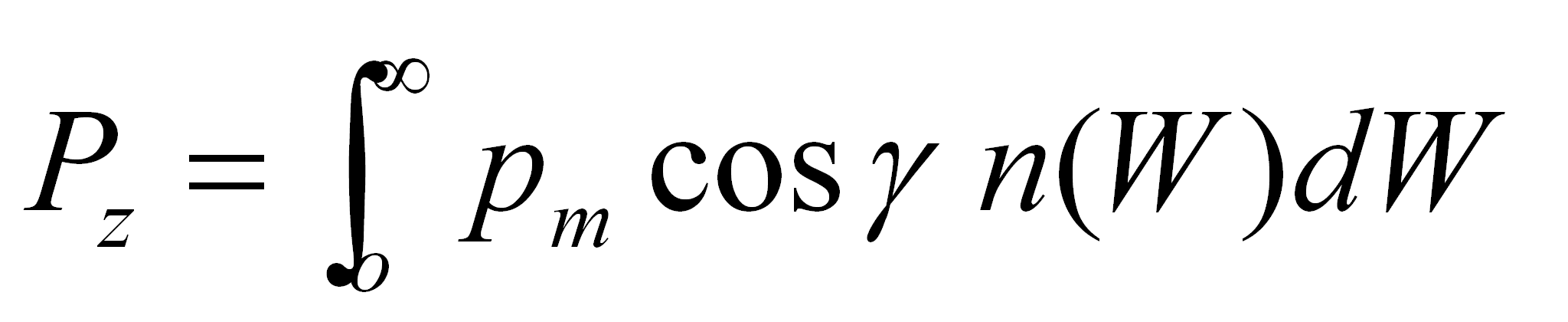                                                              (4.49c)


avec dW/dγ = p_m E_L sin γ
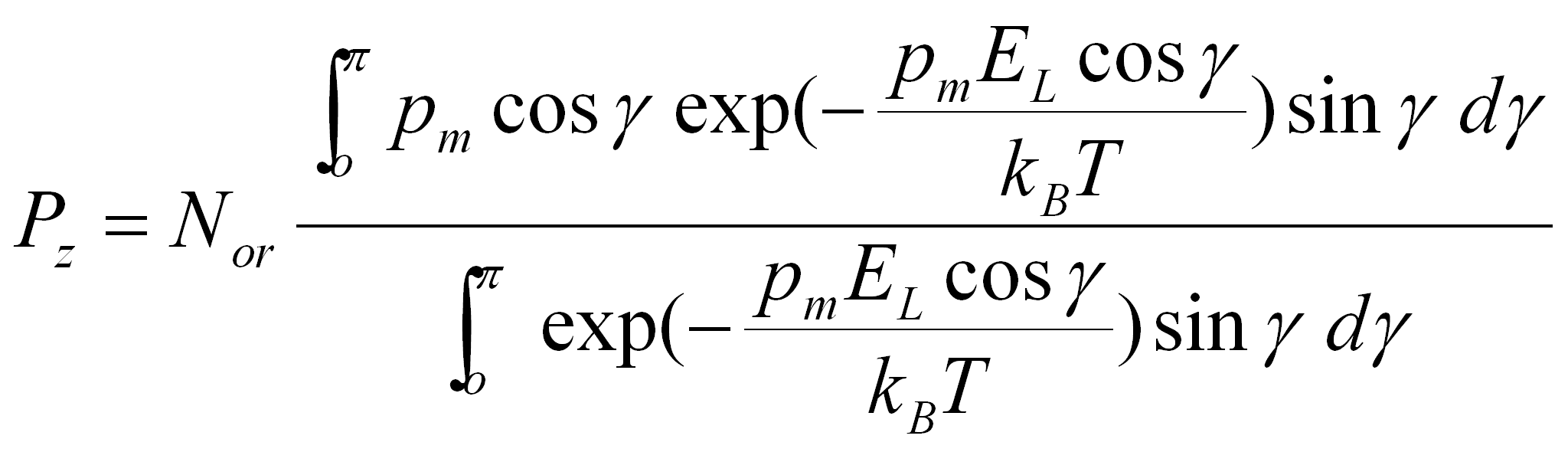                                                              (4.49d)


Formellement, cette situation est comparable à celle rencontrée dans l'étude du paramagnétisme. En transposant les résultats du calcul de la théorie de Langevin ( 3.4.2) on obtient:

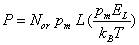                                                              (4.50)

où N_or est le nombre de molécules portant p_m, par unité de volume. L'argument de la fonction de Langevin reste en pratique toujours petit devant l'unité. En effet, pour un champ E_L = 10⁸ V/m, ce qui est une valeur très élevée, à 20C et pour un moment dipolaire typique de 510^-30 Cm, le rapport p_m E_L / k_BT vaut seulement 0,12. On peut donc représenter la fonction de Langevin par son développement (3.30) limité au premier terme. Il vient :


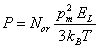                                                             (4.51)

Le facteur de polarisation par orientation _or vaut par conséquent:

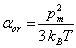                                                                               (4.52)
On appelle substances polaires celles qui contiennent des molécules possédant un moment dipolaire permanent.