Exercices

3.12 EXERCICES

3.12.1 On a mesuré la susceptibilité relative du nickel en fonction de la température (tab. 3.110).

Tableau



montrer que ces résultats sont conformes à la loi de Curie-Weiss.
Déterminer-la température de Curie. Calculer le nombre moyen de magnetons de Bohr par atome.

3.12.2 Comment varierait le moment magnétique moléculaire d'un ferrite à structure spinelle, répondant à la formule MFe₂O₄, en fonction des quantités relatives de matière présentes en structure normale et en structure inversée. Considérer les cas où M représente le manganèse, puis le nickel.

3.12.3 Calculer la largeur 1 des domaines à l'équilibre, dans l'échantillon de la figure 3.56. Comparer l'énergie magnétostatique de cette structure avec celle d'un parallèlepipède de même dimension ne possédant qu'un seul domaine. Considérer le cas du fer. Dans ce métal W_SB = 3.5 10^-3 J/m², I_s = 2.15 Wb/m². Application numérique pour a = 1 cm.

3.12.4 Le tore de la figure 3.111 est constitué d'un matériau magnétique caractérisé par les paramètres μ_ri et ν du modèle de Rayleigh. Calculer les valeurs moyennes de ces paramètres applicables au tore, en tenant compte de la variation du champ magnétique en fonction du rayon. Exprimer ces paramètres en fonction du rapport X = r_e/r_i.



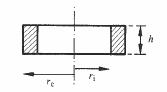
Fig. 3.111

3.12.5 Démontrer la relation (3.117) en se référant à la figure 3.79, sur laquelle on fera tendre a vers l'infini.

3.12.6 Calculer le nombre de spires et la résistance en fonction de la fréquence, à 800, 1600, 2 400, 3 200 Hz, d'une bobine de 160 mH traversée par un courant de 1 mA. Le matériau magnétique possède les coefficients de Jordan suivants : t = 2,5-10^-3 Ω/H Hz, F = 4 10^-6 Ω/H Hz², h = 4 10^-2 Ω/H Am^-1 Hz, sa perméabilité relative est de 80. La longueur moyenne d'une ligne d'induction vaut 12,6 cm, la section magnétique vaut 2 cm². La résistance de l'enroulement est de 5 Ω.