B H

3.8 LE DIAGRAMME B-H

3.8.1 Introduction

Le diagramme B-H, appelé aussi courbe d'aimantation ou cycle d'hystérésis est la courbe de réponse de matériaux magnétiques. La simplicité de l'équation B = µH n'est qu'apparente. En fait, cette relation n'est pas linéaire puisque la perméabilité µ dépend de H, d'où la nécessité d'une représentation de la fonction B(H). La non linéarité des matériaux magnétiques ne rend pas leur utilisation particulièrement aisée. Par contre, elle permet la réalisation de certains dispositifs intéressants, tels que les registres à bulles magnétiques, les mémoires magnétiques, les régulateurs à noyaux saturables, etc...

La forme du diagramme B-H dépend de la mobilité des parois de Bloch, elle-même fonction des énergies W_an, W_ms, W_ec^, W_mt et du champ H appliqué. Selon les cas, un modèle mathématique détaillé du diagramme est nécessaire, ou au contraire la connaissance d'un ou deux paramètres représentatifs est suffisante.

3.8.2 Processus de polarisation et diagramme B - H

Soit un monocristal de fer, pratiquement sans défauts, dans lequel les domaines magnétiques se présentent tels qu'à la figure 3.68 (a).



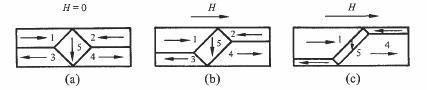
Fig. 3.68

Dès qu'on applique un champ H comme indiqué, l'énergie des moments magnétiques est augmentée dans les domaines 2 et 3, et dans une plus faible mesure dans le domaine 5. Le respect de la condition de l'énergie minimum dans l'échantillon entraîne alors une diminution du volume de ces domaines.  Dans un champ H croissant, la structure des domaines prendra donc successivement les allures représentées à la fig. 3.68 (b) puis 3.68 (c). Finalement, un seul domaine orienté selon H subsistera. Dans cette exemple idéal, le déplacement des parois de Bloch est parfaitement libre. En coupant H, on se retrouve donc à l'état initial (fig. 3.68 (a)), le processus de polarisation est réversible. Les défauts cristallins ont un effet important sur la forme du diagramme B-H. L'action de défauts ponctuels sur le déplacement des parois de Bloch, à l'intérieur d'un monocristal, est illustrée au tableau 3. 69.



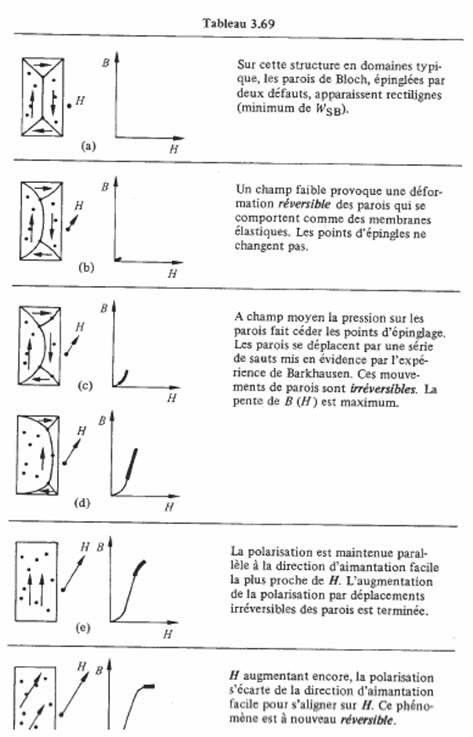
Dans un milieu polycristallin, un processus analogue à celui décrit au tableau 3.69 se produit dans chaque grain. Toutefois, la situation est compliquée par les interactions d'ordre magnétostatique et magnétostrictif existant entre grains voisins. A nouveau, la structure des grains joue un rôle très important.

La forme du diagramme B-H peut varier fortement d'un matériau magnétique à l'autre (fig. 3.70). Pour un matériau donné, elle varie en fonction des conditions d'utilisation et plus particulièrement en fonction de l'amplitude du champ magnétique (fig. 3.71).



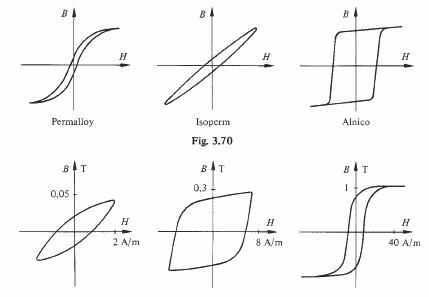
Fig. 3.71 Effets de l'amplitude du champ sur le diagramme B-H d'un alliage fer-nickel.

La fonction B(H) observée à champ croissant sur un échantillon n'ayant jamais été polarisé (à l'échelle macroscopique) porte le nom de courbe de première aimantation.

A champ décroissant, la fonction B(H) s'écarte de la courbe de première aimantation, en raison du caractère irréversible de la polarisation. En régime périodique, la fonction B(H) prend la forme d'un cycle d'hystérésis.

Seule une élévation de la température de l'échantillon au-dessus du point de Curie permet de décrire une nouvelle fois la courbe de première aimantation. La matière

magnétique garde en quelque sorte la mémoire des polarisations qu'elle a subie.

On appelle cycle d'hystérésis principal le cycle observé lors d'une variation sinusodale lente de H, d'amplitude suffisante pour conduire à la saturation. Schématiquement, le diagramme B-H se divise en trois zones:

• la zone des champs faibles (tab. 3.69 (b)) caractérisée par un comportement quasi linéaire de la matière, ainsi que des perméabilités modérées;
• la zone des champs moyens (tab. 3.69 (c), (d), (e)) dans laquelle les effets non linéaires s'accentuent fortement, tandis que la perméabilité passe pas sa valeur maximum ;
• la zone des champs forts (tab. 3.69 (f)) ou zone de saturation où la perméabilité décroît et tend asymptotiquement vers la perméabilité du vide.

Sauf dans certains monocristaux, le passage d'une zone à l'autre s'effectue progressivement. Les trois zones ne se distinguent donc pas toujours nettement les unes des autres. Il existe même certains alliages, reconnus pour leur faible variation de perméabilité en fonction de H, dans lesquels la distinction entre les zones des champs faibles et moyens est totalement effacée.

3.8.3 Induction à saturation. Définitions

L'équation (3.10), B = μ_o H + I, montre qu'il n'y a théoriquement pas de saturation de B. La limite des valeurs de B accessibles ne provient, selon (3.10), que de l'impossibilité de créer des champs H aussi grands qu'on pourrait le désirer. En fait, c'est la polarisation magnétique qui atteint une valeur de saturation, à l'échelle du domaine magnétique, si la température s'approche de 0 K ou si H -> infini. L'usage a pourtant consacré l'expression champ d'induction à saturation B_sat. Pour éviter toute incertitude, on distingue deux valeurs de B_sat.

B_sat valeur pratique est la valeur maximum de I, que le matériau magnétique permet d'atteindre au prix d'une dépense raisonnable de potentiel magnétique. Pour être une donnée cohérente, B_sat valeur pratique doit être complétée par l'indication du champ H_sat correspondant.

B_sat valeur théorique correspond à la valeur de saturation de I, soit encore

B_sat valeur théorique = lim (B - μ_o H)                                        (3.100)

Dans un alliage Fe - Si à 4% de Si par exemple, B_sat valeur pratique = 1,80 T à H= 800 A/m.

3.8.4 Induction rémanente et champ coercitif. Définitions

Soit un échantillon polarisé à saturation, c'est-à-dire soumis à un champ magnétique H supérieur à H_sat.

On appelle induction rémanente B_r, l'induction qui subsiste dans l'échantillon après qu'on ait fait décroître H jusqu'à zéro.

On appelle champ coercitif H_c le champ magnétique nécessaire pour annuler l'induction rémanente.

L'induction rémanente et le champ coercitif sont des propriétés spécifiques du matériau considéré. Elles figurent sur le cycle d'hystérésis principal. Il faut remarquer que B_r représente l'induction maximum pouvant subsister après disparition d'un champ magnétique. Mais il est évident que le phénomène de la rémanence existe également pour des champs maxima inférieurs à H_sat. Alors, l'induction qui subsiste après disparition du champ est inférieur à B_r.

3.8.5 Définition de quatre perméabilités relatives

La non-linéarité de la fonction B(H) a pour effet que la perméabilité relative définie par (3.14) n'est pas une constante, mais une fonction du champ magnétique. La connaissance complète de cette fonction μ_r(H) n'est pas toujours indispensable.

Dans de nombreux calculs, la perméabilité apparaît simplement sous la forme d'un nombre. On distingue alors quatre perméabilités scalaires (fig. 3.72).



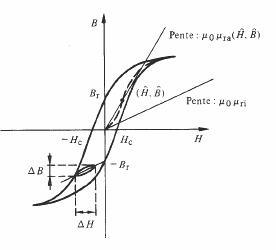
On appelle perméabilité relative initiale µ_ri le quotient

                                                                (3.101)

déterminé sur un échantillon n'ayant jamais subi de polarisation irréversible.

La perméabilité relative initiale est une valeur théorique, inaccessible directement par la mesure puisqu'elle correspond à un champ nul. Il faut donc la déterminer par extrapolation. En pratique, on donne souvent pour µ_ri la perméabilité relative mesurée dans un champ faible, compris entre 100 et 200 A/m par exemple.

On appelle perméabilité relative amplitude la perméabilité relative dans la région des champs moyens, définie par

                                                       (3.102)

les valeurs de B et H étant relevées sur la courbe de première aimantation.

C'est une bonne approximation de la perméabilité relative qui serait effectivement observée dans un champ alternatif basse fréquence, d'amplitude H. Une valeur plus précise ne peut être obtenue que par la mesure ou le calcul au moyen d'un modèle mathématique du diagramme B-H.

Considérons maintenant le cas où un champ alternatif H₂ est superposé à un champ continu H₁a gissant parallèlement à H₂. Si H₂ > H₁, le diagramme B-H est simplement translaté sans déformation notable. Si H₂ << H₁ on observe l'apparition d'un cycle local totalement excentré. La position de ce cycle est variable et ne dépend pas seulement de H₁ et H₂ mais encore de la façon dont ces champs ont été appliqués: par valeurs croissantes ou décroissantes par exemple. Dans tous les cas les cycles locaux sont inscrits dans le cycle principal.

En présence d'un champ continu superposé H_l on appelle perméabilité relative différentielle μ_rΔ le rapport

                                                                                 (3.103)

où ΔH est l'amplitude du champ alternatif et ΔB la variation correspondante de l'induction magnétique.

On appelle perméabilité relative réversible μ_rr,la valeur de la perméabilité relative différentielle pour un champ alternatif rendant vers zéro, soit:

                                         (3.104)

Dans tous les développements de portée générale, la perméabilité relative est désignée simplement par le symbole μ_r.

3.8.6 Matériaux magnétiques doux et durs. Définitions.

On appelle matériaux magnétiques doux ceux dans lesquels le champ coercitif est petit (tab. 3.106, 3.107 et 3.108). La surface de leur cycle d'hystérésis principal est faible. Le permalloy et l'isoperm (fig. 3.70) sont deux exemples de tels matériaux.

On appelle matériaux magnétiques durs ceux dans lesquels le champ coercitif est élevé (tab. 3.109). La surface de leur cycle d'hystérésis principal est importante, comme celle de l'Alnico représentée à la figure 3.70. Dans ces matériaux, les parois de Bloch sont fortement épinglées.

Les impuretés et autres défauts entravant le mouvement des parois de Bloch gênent aussi le déplacement des dislocations. C'est pourquoi les matériaux magnétiques durs sont également durs au sens mécanique.

3.8.7 Pertes magnétiques. Généralités.

Toute variation d'induction dans une matière magnétique provoque, à l'intérieur de celle-ci, une dissipation d'énergie. Cette énergie apparaît le plus souvent sous forme de chaleur et n'est généralement pas récupérable, d'où l'expression pertes magnétiques utilisée pour désigner le phénomène. On distingue trois types de pertes magnétiques

• les pertes par hystérésis,
• les pertes par courant de Foucault,
• les pertes résiduelles ou pertes par traînage.

Les pertes par hystérésis sont dues au travail des forces de freinage agissant sur les parois de Bloch en mouvement. Elles sont donc maximum quand les forces d'épinglage sont les plus grandes, c'est-à-dire dans les matériaux magnétiques durs. Les pertes par hystérésis correspondent au travail nécessaire pour parcourir lentement le diagramme B-H.

On appelle perte par courant de Foucault, les pertes par effet Joules résultant des courants créés dans toute matière conductrice (magnétique ou non), par un flux variable dans le temps. Ces pertes peuvent être importantes dans les matériaux de faible résistivité électrique comme les alliages magnétiques, elles restent à un bas niveau dans les ferrites.

Les pertes par traînage sont dues au retard de l'induction par rapport au champ, décrit à la figure 3.73.



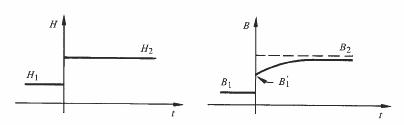
Fig. 3.73

Lorsque le champ H varie brusquement de H₁ à H₂, l'induction suit immédiatement de B₁ à B₁' puis tend asymptotiquement vers la valeur de B₂ correspondant à H₂. Deux mécanismes différents peuvent être à l'origine de ce phénomène.

Le processus de traînage par fluctuations thermiques est le suivant:

A la suite du mouvement initial des parois de Bloch dû à la transition de H₁ vers H₂, les forces créées sur certains points d'épinglage sont suffisamment voisines de celles nécessaires au décrochement pour que celui-ci se produise, après un certain temps, sous l'action des fluctuations locales de la polarisation. En effet, la polarisation n'a pas exactement la même direction en tout point d'un domaine, comme en témoigne la décroissance de I(T) quand la température s'élève (fig. 3.20). Cette direction, fluctuant au cours du temps, affaiblit tantôt l'effet du champ extérieur, tantôt le renforce, faisant céder les points d'épinglage les plus sollicités, jusqu'à la disparition complète de ceux-ci et la stabilisation de B.

Le traînage par diffusion se rencontre de façon typique dans le fer a contenant du carbone (fig. 3.74). Les atomes de carbone se placent en position interstitielle, sur les arêtes et au centre des faces du cube. On distingue 3 familles x, y et z de sites susceptibles d'être ainsi occupés.

Supposons que seuls les sites x sont occupés, le cristal se trouvera dilaté selon x. Si la polarisation est orientée selon x, l'énergie magnétostrictive sera abaissée, à condition



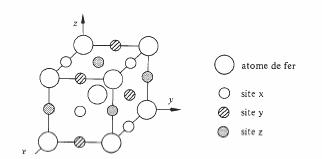
que la substance présente une magnétostriction positive. Il y a donc interaction entre la structure des domaines magnétiques et la position des atomes de carbone. En particulier, un changement de polarisation provoque une diffusion d'atomes abaissant l'énergie interne du système, qui modifie à son tour la polarisation, etc. Ce phénomène ne pouvant être instantané, il provoque le traînage par diffusion.

3.8.8 Modèle du diagramme B-H pour les champs faibles

Sauf dans certains cas peu intéressants en pratique, il n'est pas possible d'établir de façon purement théorique la fonction B(H) relative à un matériau donné. Il reste par conséquent à trouver les équations représentant le mieux possible les fonctions B(H) établies expérimentalement.

A champs faibles, tous les matériaux magnétiques présentent un comportement analogue. On dispose, pour cette raison, de modèles d'usage général dont seuls les paramètres caractéristiques changent d'une matière à l'autre. Le modèle le plus utilisé, en raison de sa grande simplicité et de la qualité satisfaisante des résultats qu'il fournit, est le modèle de Rayleigh.

Ce modèle donne une expression de la perméabilité en fonction du champ ainsi qu'une équation décrivant le cycle d'hystérésis.

En fonction de l'amplitude H du champ, la perméabilité présente toujours une variation du type représenté à la figure 3.75.



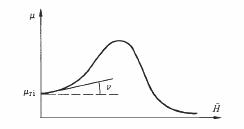
Fig. 3.75

Pour les petites valeurs de H, la perméabilité est donc assimilable à une fonction linéaire

µ_rR = µ_ri + ν H                                                           (3.105)

On appelle µ_rR la perméabilité relative de Rayleigh et n le coefficient de Rayleigh. L'expression (3.105) ne tient pas compte de la variation de la perméabilité en fonction de la fréquence, étudiée au paragraphe 3.8.12.

En multipliant les deux membres de (3.105) par µ₀H, on obtient l'équation de la courbe de première aimantation

B = µ_o µ_rH + νµ₀H²                                                                           (3.106)

sur laquelle se trouve une extrémité du cycle d'hystérésis. Pour une valeur de H considérée, le cycle d'hystérésis de Rayleigh s'obtient de la manière suivante (fig. 3.76).

• On trace à partir du point B,H de la courbe de première aimantation, une droite passant par l'origine. Son équation s'écrit :
  
  B= µ_o (µ_ri + ν H) H                                       (3.107)
  
  où Bet H représentent les valeurs instantanées des champs d'amplitudes B et H.
• On reporte ensuite, de part et d'autre de cette droite et parallèlement à l'axe des inductions, deux segments égaux par l'extrémité desquels passera le cycle. La longueur de ces segments doit être nulle en H = H' et maximum en H = 0. Rayleigh observa que cette longueur pouvait encore s'exprimer en fonction de ν et posa l'équation du cycle sous la forme B = µo [(µ_ri + ν H) H ν/2(H² - H²)]        (3.108) Le signe + correspond à la branche supérieure du cycle, le signe - à la branche inférieure.

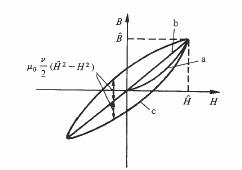
Fig. 3.76 Etablissement du cycle de Rayleigh:

Le changement de signe dans (3.108) n'est pas pratique dans les calculs, mais on peut le supprimer par un développement en série de Fourier. Ce procédé est particulièrement adapté au cas où H est sinusodal, comme dans l'exemple d'application traité au paragraphe 3.8.18.

3.8.9 Pertes par hystérésis à champ faible

L'énergie W_h correspondant aux pertes par hystérésis, dissipée par unité de volume, lorsqu'on parcourt le cycle une fois, vaut

W_h =   B ^.dH                                (3.109)

Cette intégrale représente la surface du cycle. En admettant pour celui-ci la représentation de Rayleigh il vient, par (3.108)

W_h = f µ_o ν (H²-H^z)dH = 4µ_o νH³ /3                J/m³       (3.110)

Dans un noyau caractérisé par une section S du flux magnétique et une longueur moyenne l des lignes de B, la puissance P_h perdue par hystérésis à la fréquence n vaut :

P_h = W_h S l f                                                    (3.111)

Une inductance qui ne présenterait que des pertes par hystérésis peut être représentée par le schéma équivalent suivant :



Fig. 3.77

On choisit la résistance R_h telle que la puissance qui s'y dissipe par effet Joule soit égale à P_h. Cette résistance, ainsi que l'angle de pertes par hystérésis défini par

tan δ_h = R_h / wL                                                                (3.112)

se déduisent aisément de ce qui précède. Soient N le nombre de spires de l'inductance, i la valeur efficace du courant sinusodal de pulsation w qui la traverse. On a

P_h = R_h i ²;                                                                 (3.113)

et

I = H l / N SQR(2)                                                                   (3.114)

En portant (3.110) dans (3.111) et en identifiant le résultat à (3.113) il vient:

tan δ_h = 4 ν B / 3 π μ_oμ_rR²                                      ;        (3.115)

3.8.10 Pertes par courants de Foucault

Les pertes par courants de Foucault P_F dans un noyau de résistivité p et de volume V se calculent par la relation

P_F =  ρ i_c² dV                                                              (3.116)

où i, représente la densité des courants de Foucault, en valeur efficace. L'intégration de (3.116) mène toujours à des développements laborieux, mais sauf cas rares, on peut faire usage de formules approchées. En effet, dans le but de diminuer les pertes par courants de Foucault, les circuits magnétiques sont le plus souvent divisés en éléments isolés électriquement les uns des autres. Pour des raisons de fabrication évidentes, ces éléments affectent toujours des formes simples (fig. 3.78) : tôle, rubans, fils circulaires, fines particules dans les noyaux comprimés ( 3.9.8).

Il suffit donc de calculer (3.116) pour chaque forme d'élément susceptible d'être utilisée pour la constitution d'un noyau magnétique.



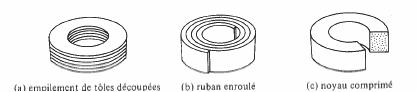
Fig 3.78 Trois façons de réduire les pertes par courants de foucault dans un tore.

Soit le cas d'une tôle soumise à un champ magnétique orienté selon l'axe z

 H= Re kH₀ exp j wt (fig. 3.79).



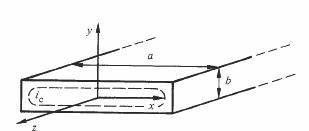
Si  b << a, la résolution des équations de Maxwell donne, pour le phaseur du champ magnétique dans la tôle

                                                                     (3.117)

où

                                                                      (3.118)

Dans ces expressions, ω désigne la pulsation de H, ρ la résistivité de la tôle. L'équation rot H = E / ρ se réduit à:

                                                             (3.119)

En tirant i_c, de (3.119) et (3.117), on obtient par (3.116), les pertes volumiques par courants de Foucault p_F

p_F = (B ω b)² /2 α ρ                                                              (3.120)

Cette formule est valable tant que la diminution des courants de Foucault liée à l'atténuation de H_z à l'intérieur de la tôle (3.117) reste négligeable. L'égalité correspond au cas théorique d'une atténuation nulle. L'expression (3.120) est encore valable dans le cas d'une sphère ou d'un cylindre, dans les conditions résumées au tableau 3.80.

Tableau 3.80
Tôle d'épaisseur b < 1/b	a =	3
Cylindre infiniment long, de rayon b < SQR(r/w mo µr)	a =	8
Sphère de rayon b < SQR(r/w mo µr)	a =	10

Dans une tôle de fer silicié, typiquement μ_r = 5000 et ρ = 0.6 10^-6 Wm, donc 1/β = 0.75 mm à 50 Hz et 0.075 mm à 5 kHz.

Il est souvent indiqué de représenter les pertes par courant de Foucault par une résistance R_F placée dans un circuit équivalent série. On définit alors un angle de perte par courants de Foucault δ_Fdonné par:

tan δ_F = R_F / ωL                                                            (3.121)

En procédant comme dans le cas des pertes par hystérésis, on déduit de (3.120),

tan δ_F = μ_o μ>_r b² ω /α ρ                                                 (3.122)

Les pertes par courants de Foucault données par (3.120) sont des pertes volumiques, elles ne dépendent pas de la forme ou de la taille du noyau, mais seulement de la forme et de la taille des éléments magnétiques qui le constituent.

3.8.11 Remarques

La perméabilité d'une tôle varie généralement en fonction de l'angle de B avec la direction de laminage (fig. 3.92). Avec la solution représentée à la figure 3.78 (a), on ne peut donc exploiter la perméabilité maximum de la tôle, B tournant de 360 par rapport à la direction de laminage lorsqu'on décrit une ligne de champ. La solution représentée à la figure 3.78 (b), utilisée avec un matériau à perméabilité maximum dans le sens de laminage ne présente pas cet inconvénient.

La perméabilité relative d'un noyau comprimé est limitée, par l'entrefer séparant chaque grain, à des valeurs de l'ordre de 100 au maximum. Mais la taille réduite des grains permet une utilisation à des fréquences plus élevées que les deux solutions précédentes.

3.8.12 Correction de la perméabilité

Les courants de Foucault provoquent non seulement des pertes mais encore une diminution apparente de la perméabilité, liée à l'atténuation du champ magnétique à l'intérieur de la matière. La valeur de H à l'intérieur d'une tôle se déduit de (3.117), en faisant usage de la relation (3.123) :

cosh [( 1 + j )x] = SQR(- (cosh 2x + cos 2x) / 2)

Le résultat est représenté à la figure 3.81, pour quelques valeurs du produit bb.

 

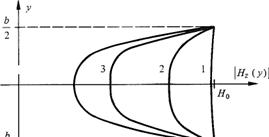
L'induction moyenne, dans la tôle est donc inférieure à µ_oµ_r(H_o)H_o. Elle vaut:

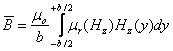                                                       (3.124)

Cette intégrale ne se calcule aisément que lorsque µr (Hz) peut être considérée comme constante dans -b/2 < y < + b/2. Cette condition n'est pas trop limitative, elle correspond en fait à la situation dans laquelle une tôle est utilisée convenablement. On trouve alors

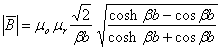                                                             (3.125)

La correction de µr apparaît clairement dans cette équation, qui sert également à étendre le domaine de validité de (3.120). En remplaçant dans cette dernière B par IB I calculé selon (3.125), l'expression (3.120) peut être utilisée jusqu'à b = 2/(3. L'erreur sur P_F est alors de 2,4% par défaut [41].

3.8.13 Discrimination expérimentale des types de pertes

Les équations (3.115) et (3.122) montrent que tan δ_h ~ B et tan δ_F ~ ω. Il est donc possible de séparer ces deux types de pertes en mesurant, au moyen d'un pont de Wheatstone, la tangente de l'angle des pertes magnétiques totales. Pour la plupart des matériaux, on obtient un graphique, appelé diagramme de Jordan, qui présente l'allure suivante (fig. 3.82)



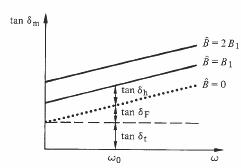
Fig. 3.82 Décomposition des pertes à ω = ω_o et B' = B₁

La valeur de tan δ_m ne s'annule pas lorsque ω → 0 et B' → 0 en raison de l'existence des pertes par traînage. Lorsque ces dernières ne dépendent pratiquement pas de B' et de ω, tan δ_m (B', ω) est un réseau de droites parallèles. La distance entre deux droites voisines est invariable si l'augmentation de B' se fait avec un pas constant. Mais c'est là un cas idéal: Le plus souvent, la tangente de l'angle de pertes par traînage, tan δ_t varie dans une certaine mesure en fonction de B' et ω. Il en résulte une distorsion plus ou moins importante du diagramme de Jordan par rapport à sa représentation à la figure 3.82. La séparation de tan d_h, tan δ_F et tan δ_t, ne peut plus dans ces conditions se faire d'une façon absolument rigoureuse.

3.8.14 Modèles généraux pour les pertes à champ faible

Plusieurs modèles équivalents, dans lesquels tan St est considéré comme indépendant de Ê et w, sont en usage pour évaluer les pertes magnétiques totales. Les trois types de pertes sont traités séparément les uns des autres, puis sommés. En reprenant les résultats de calcul obtenus dans les paragraphes précédents, on peut écrire le facteur de pertes tan δ/µ sous la forme :

                                                   (3.126)

coefficients k₁ et k₃ concernent les pertes par hystérésis et par traînage. Ce sont des caractéristiques du matériau. Le coefficient k 2 concerne les pertes par courants de Foucault. Il dépend non seulement du matériau, mais encore de la forme du noyau ou des éléments qui le constituent.

Le modèle de Jordan (3.128) correspond à l'équation 3.127 dont les deux membres seraient multipliés par µ_rR w/2pL. Il fournit donc les pertes sous la forme d'une résistance R_m placée dans un circuit équivalent série du type de la figure (3.77).

R_m = h H f L + F f²L + t f L                                                   (3.128)

h [Ω / HA m^-1 Hz], F[Ω / HHz²] et t[Ω / HHz] sont les coefficients de Jordan, souvent donnés dans la littérature en d'autres unités que celle du Système International. Le champ magnétique H est exprimé en valeur efficace.

En multipliant les deux membres de (3.127) par 2p/µ_o, on tombe sur le modèle de Legg.

                                                          (3.129)

a [ 1 / Wb m^-2 ], e [s], c [1] sont les coefficients de Legg.

On exprime encore les pertes magnétiques par le truchement d'une perméabilité relative complexe 11r définie dans le cas d'un circuit équivalent série par:

                                                    (3.130)

En décomposant μ_r en ses parties réelle et imaginaire de façon qu'à R_m>0 corresponde μ''_r > 0

μ_r = μ'_r - j μ_r''                                                                (3.131)

On a :

                                                    (3.132)

et

                                                         (3.133)

Le fait qu'un relevé des pertes en fonction de B et ω ait l'allure de la figure 3.82 démontre la validité du modèle (3.127) pour les calculs de l'ingénieur. Toutefois la division des pertes en trois catégories indépendantes les uns des autres et fonction chacune d'une variable différente est artificielle. Cette procédure est en contradiction avec la réalité physique. En effet, le cycle d'hystérésis n'est pas seulement déterminé par B. Pour un B donné, il s'élargit selon l'axe H quand la fréquence augmente, il varie aussi avec la forme de H, sinusodale, carrée, triangulaire, etc. L'observation cinématographique du mouvement des parois de Bloch [42] dans un champ alternatif donne une vision utile de ces phénomènes, dont l'interprétation détaillée demeure complexe. Jouent un rôle important la vitesse de déplacement des parois de Bloch entre deux points d'épinglage successifs, et le fait que la taille moyenne des domaines diminue quand la fréquence augmente. Dans (3.127) l'accroissement de tan δ_h avec la fréquence est formellement reporté sur tan δ_F.

Le calcul de tan δ_F par (3.122) n'est pas entièrement correct non plus, même dans le domaine d'application défini ci-dessus pour cette formule. Dans la démonstration de celle-ci, la présence des domaines magnétiques n'est pas prise en considération. L'induction est donc implicitement supposée varier de façon continue. Or B varie localement de façon quasi discontinue, sous l'effet du déplacement saccadé des parois de Bloch. Il est tentant de voir dans ce phénomène l'origine de courants de Foucault plus intenses que prévu. L'écart entre les pertes par courants de Foucault déterminées par (3.122) et celles mesurées sur un diagramme de Jordan porte de nom de pertes par courants de Foucault anormales. Ces dernières restent faibles à champ faible, une correction de (3.122) ne s'impose donc que dans les champs moyens à fort, ce qui renforce la crédibilité de l'interprétation qui vient d'être donnée.

En réalité les pertes par traînage, par hystérésis aussi bien que par courants de Foucault dépendent de la dynamique des parois de Bloch. Théoriquement, un modèle adéquat de ces parois devrait permettre de calculer globalement les pertes, mais les modèles en usage en physique sont encore largement insuffisants pour remplacer avec profit l'équation (3.127), du point de vue de l'ingénieur.

3.8.16 Pertes magnétiques à champs moyens et forts

Dans les champs moyens et forts, le cycle d'hystérésis cesse d'être représentable par le modèle de Rayleigh et les pertes par courants de Foucault anormales peuvent atteindre plusieurs fois la valeur théorique donnée par (3.120). Par contre, la contribution des pertes par trainage devient négligeable en valeur relative. Dans ces conditions, on calcule les pertes à partir d'une expression empirique du type:

p = η B^af + e B² f²                       >W/kg                  (3.134)

Le premier terme représente les pertes par hystérésis évaluées selon la formule de Steinmetz. Dans le cas du fer silicié, a = 1,6, η varie approximativement entre 5^.10^-4 et 4^.10^-3 selon le pourcentage de Si et le traitement thermique. La formule est applicable pour 0,2T < B < 1,5 T. De nombreuses mesures montrent que son usage peut être étendu à presque tous les matériaux magnétiques, y compris les ferrites, à condition que la fréquence reste faible, par exemple inférieure à 100 Hz. La valeur de a reste toujours voisine de 1,6. La plage de B dans laquelle le modèle est utilisable dépend d'une part de B_sat, d'autre part de l'étendue du domaine de Rayleigh, dans lequel les pertes par hystérésis sont proportionnelles à B³ et non à B¹'⁶ (3.110). La particularité étonnante de la formule de Steinmetz est qu'elle ne contient pas la perméabilité.

Le deuxième terme de (3.134) représente les pertes par courants de Foucault. Le coefficient e ne peut être calculé théoriquement.

Quand le matériau magnétique se présente sous la forme d'une tôle, on détermine le plus souvent e, puis η et a si nécessaire, au moyen de l'appareil d'Epstein (fig. 3.83).



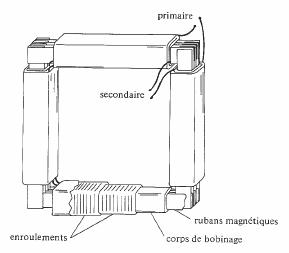
Fig. 3.83 Appareil d'Epstein

La tôle à étudier est découpée en rubans, empilés pour former quatre prismes. Munis chacun d'un enroulement primaire et d'un enroulement secondaire, ces prismes sont ensuite assemblés pour former un circuit magnétique fermé, de forme carrée. Des précautions doivent être prises pour éviter la formation d'entrefers dans les angles. Les quatre enroulement primaires, respectivement secondaires sont branchés en série et intégrés dans le circuit de mesure de la figure 3.84.



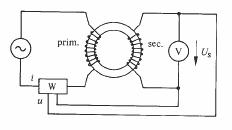
Fig. 3.84

L'appareil d'Epstein fonctionne donc comme un transformateur à vide, à la consommation des instruments près. La tension U_S est une mesure de B, la fréquence et la section magnétique étant connus. Le wattmètre indique directement les pertes magnétiques totales. Les pertes cuivre dans le primaire ne sont pas prises en compte par le wattmètre, puisque son circuit de tension est branché au secondaire.

Le coefficient a étant supposé connu, les pertes par hystérésis et par courants de Foucault sont facilement dissociées les unes des autres. En divisant (3.134) par f il vient:

   p/f = n B^a + e B² f                                                              (3.135)

Selon le modèle, les points expérimentaux de la fonction p/f doivent donc s'aligner sur une droite de pente eB2, dont l'intersection avec l'axe vertical détermine n (fig. 3.85).



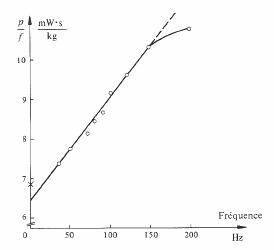
Fig. 3.85 Pertes magnétiques totales par cycle, dans le Permalloy 45; (45 % Ni + 55 % Fe). Epaisseur de la tôle : 0,15 mm, µ_r = 20 000, à = 1 T [29].

La figure 3.85 est une vérification de la validité de (3.134), elle montre cependant que le modèle n'est plus applicable au-delà d'une certaine fréquence. Si a n'est pas connu, il suffit pour le déterminer d'effectuer deux séries de mesures, avec des valeurs de B différentes.

Les ferrites ne peuvent évidemment pas être placés dans un appareil d'Epstein, mais le principe de la mesure est conservé pour ces matériaux.

Le calcul des pertes à champs moyens et forts tel qu'il vient d'être présenté peut paraître un peu sommaire. Mais il ne faut pas oublier que les exigences sont ici moins grandes qu'à champ faible. Souvent la fréquence est fixe, de même que l'amplitude de B, et seules les pertes totales ont une importance. D'autre part, la variation possible des paramètres magnétiques et électriques d'un lot de fabrication à l'autre, peuvent rendre aléatoires les résultats de calculs plus raffinés.

Si les pertes doivent néanmoins être calculées avec une plus grande précision (erreur maximum tolérée de l'ordre de quelques pour-cent par exemple) il n'y a pas d'autre méthode que la résolution par voie numérique des équations de Maxwell, rendues non linéaires par la présence de la fonction B (H). Une solution de ce type est présentée dans [43] pour le cas d'une plaque infinie. Le champ H sinusoidal est imposé selon y (fig. 3.86).



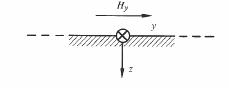
Fig. 3.86

La courbe de première aimantation est décrite par la fonction H

B = H / (a + b H )                                                               (3.136)

où a et b sont des caractéristiques du matériau, déterminées par la mesure. Par exemple, pour un alliage de fer contenant 36 % de Ni et 6 % de Cr, dont la résistivité vaut 2,5.10-' fl m, on a les valeurs suivantes : a = 1,5.103 m/H et b= 0,47 T-I. A l'extérieur du domaine H_sat < H < H_sat, (3.136) est remplacée par

B = m_o H + I_sat           pour         H > H_sat                                             (3.137)

B = m_o H - I_sat           pour          H> -H_sat

Le cycle d'hystérésis est décomposé en segments obtenus chacun par une translation et une déformation particulière de tronçons de la courbe de première aimantation.

Dans [44] seule la description du cycle d'hystérésis est abordée. Ce dernier est représenté par une équation différentielle, établie de façon axiomatique à partir de considérations générales portant sur les symétries du cycle. Le modèle ainsi obtenu est destiné à un usage aussi large que possible. En principe il est capable de représenter tous les matériaux, de la tôle de transformateur au ferrite à cycle rectangulaire utilisé dans les mémoires. Tous les types de modulation, avec et sans polarisation continue peuvent être considérés.

3.8.17 Pertes magnétiques dans leschamps tournants

Une approche différente est nécessaire quand, l'amplitude du champ restant constante, c'est son orientation qui varie dans le temps. Ce cas se rencontre par exemple à la jonction des circuits magnétiques des transformateurs triphasés et dans la denture des machines tournantes. On trouvera dans [45] plusieurs références concernant des mesures et des tentatives de modélisation des pertes en champs tournants.

3.8.18 Distorsion de signaux

Les signaux qui parcourent des éléments de circuits utilisant des matériaux magnétiques subissent une distorsion, du fait que B(H) n'est pas une fonction linéaire. Cette question sera abordée par le biais du problème suivant:

Soit un transformateur dont le primaire est alimenté par une source de courant I =Î cos wt. Calculer l'induction magnétique et le taux d'harmonique 3 dans la tension induite apparaissant au secondaire en circuit ouvert, sachant qu'on reste dans le domaine des champs faibles.

La source provoque donc un champ:

                                                                 (3.138)

En introduisant cette expression dans le modèle de Rayleigh (3.108) il vient:

                                                (3.139)

En remarquant que B = B pour wt = 0 et B = B_r pour w t = p / 2, on simplifie l'écriture en posant

                                                          (3.140)

où

                                              (3.141)

Il reste à développer cette expression, ou plus précisément son terme B_r sin ² w t en série de Fourier pour connaître le spectre des harmoniques de B. Le choix du signe est lié au sens dans lequel le cycle d'hystérésis est naturellement décrit, conformément à la figure 3.87.



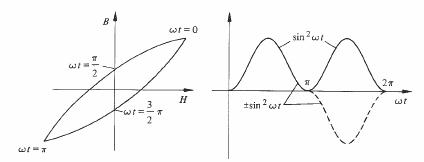
Fig 3.87

La fonction sin² wt est donc impaire, son développement ne contiendra que des termes en sinus.

                                                 (3.142)

où

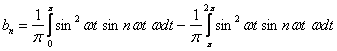                               (3.143)

Ces intégrales s'annulent pour n pair. Pour n = 1 et n = 3 elles se calculent aisément, les résultats correspondant à des valeurs plus élevées de n s'obtenant par récurrence. On trouve

      (3.144)

Le rapport de l'amplitude du 3e harmonique à celle du fondamental s'obtient en regroupant dans (3.144) les termes en sin et cos par les relations

A coswt B sinwt = C sin (wt-f)

où

                                               (3.146)

Il vient:

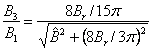                                                    (3.147)

Sauf exception, on utilise dans les transformateurs des matériaux magnétiques doux, donc B_r << B. En remplaçant B_r et B par leurs valeurs selon (3.141)

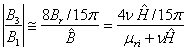                                            (3.148)

Dans le domaine des champs faibles, l'augmentation de la perméabilité due au champ magnétique, mesurée par vH, est toujours petite par rapport à µ_ri.Grâce à (3.115), (3.148) se réduit donc à

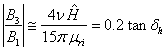                                                (3.149)

Finalement

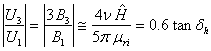                                                            (3.150)

3.9 MATÉRIAUX MAGNÉTIQUES DOUX

3.9.1 Introduction

Cette section et la suivante sont consacrées aux principales catégories de matériaux magnétiques disponibles sur le marché. On présentera successivement le fer pur, le fer allié au silicium, le fer allié au nickel, les alliages spéciaux, les ferrites et les noyaux comprimés. Quelques brèves indications concernant les applications seront fournies.

Les valeurs numériques ne devront être considérées qu'à titre indicatif. On se rappelle en effet que les propriétés magnétiques résultent d'un grand nombre de facteurs dont la composition chimique, les traitements mécaniques, les traitements thermiques sont les plus importants. C'est pour cette raison que deux matériaux de provenances différentes, mais identiques si l'on s'en réfère aux données des catalogues, peuvent présenter pour certaines caractéristiques des divergences sensibles. Quelques noms commerciaux des matériaux les plus importants seront indiqués entre parenthèses. On trouvera une liste complète de ces noms, avec l'indication des fournisseurs correspondants, dans [45].

Tableau 3.88 D'après [291].

Element	Solubilité en %
Carbone	0,007
Oxygène	0,01
Soufre	0,02
Azote	0,001
Phosphore	1,0

Sauf affinage spécial, leur concentration est assez largement supérieure aux valeurs indiquées ci-dessus, ce qui provoque l'apparition d'inclusions diverses sous forme de carbures, de nitrures, d'oxydes de fer, etc. (Fe₃C, Fe₄N, FeO). Ces inclusions freinent le mouvement des parois de Bloch, la perméabilité reste par conséquent modeste μ_ri = 200; μ_{r max} = 5 000, et les pertes élevées : 10^-12 W/kg à B = 1,5 T et f = 50 Hz.

Avec le temps certaines impuretés restées en solution solide (C et N en particulier) peuvent diffuser en direction des inclusions auxquelles elles se fixeront. La diffusion du carbone provoque une lente diminution de la perméabilité, appelée : désaccommodation. Ce processus est réversible, c'est-à-dire qu'un traitement thermique peut faire remonter la concentration de carbone en solution solide à sa valeur initiale. La précipitation des nitrures provoque également une baisse lente de la perméabilité appelée : vieillissement magnétique. Ici le processus est irréversible.

La purification du fer en améliore les qualités magnétiques de manière spectaculaire dès que la concentration des impuretés devient suffisamment basse pour qu'elles restent partout en solution solide. Sous cette forme, les impuretés ne peuvent plus gêner le déplacement des parois de Bloch, dont l'épaisseur est de l'ordre de 150 distances interatomiques ( 3.7.9). L'élimination du carbone, de l'azote et de l'oxygène s'obtient par un recuit de plusieurs heures sous atmosphère d'hydrogène. Des perméabilités relatives maxima de 0,3^.10⁶ pour un polycristal et de 1,5^.10⁶ pour un monocristal de fer ont ainsi été obtenues en laboratoire. L'utilité pratique de ces hautes perméabilités est cependant réduite, en raison du coût élevé des techniques à mettre en oeuvre pour les obtenir.

Souvent trop cher ou de qualité trop modeste, le fer non allié possède néanmoins ses domaines d'utilisation privilégiés. On peut citer, par exemple, la fabrication de pôles d'aimants dont les plus gros spécimens pèsent plusieurs milliers de tonnes. Le fer doux ordinaire s'impose ici par son rapport perméabilité/coût particulièrement favorable, et du fait que les pertes magnétiques n'entrent pas en considération (B = constante). Les mêmes raisons motivent, à une autre échelle, l'utilisation du fer doux dans l'industrie des relais électromécaniques. Enfin, le marché important des appareils directement destinés aux consommateurs fait un large usage du fer doux dans tous les moteurs, car ici un bas prix est jugé plus important qu'un bon rendement énergétique.

3.9.3 Fer silicié

L'adjonction de quelques pourcents de silicium dans un fer doux améliore plusieurs de ces qualités

• La perméabilité relative augmente
• le champ coercitif H_L diminue considérablement, ce qui entraîne une réduction des pertes par hystérésis,
• la résistivité électrique augmente, et par conséquent les pertes par courants de Foucault diminuent,
• la stabilité des caractéristiques magnétiques dans le temps s'améliore nettement.

Le seul paramètre magnétique influencé défavorablement par la présence du silicium est l'induction à saturation, qui diminue légèrement (fig. 3.89).



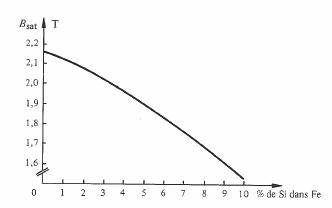
Fig. 3.89

Cet inconvénient est largement compensé par les avantages énumérés. Un autre effet du silicium est de rendre le fer cassant. Au delà de 5% de silicium, il devient si fragile qu'il est impossible de le travailler comme en témoigne la diminution de l'allongement avant rupture (fig. 3.90).



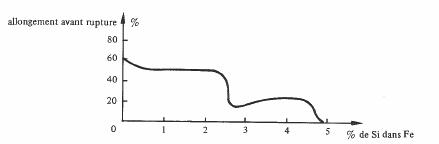
Fig. 3.90 D'après [29]

Le plus souvent, les alliages contenant 1 à 2,5 % de silicium sont utilisés dans les moteurs, générateurs et autres machines tournantes alors que les alliages à 3-4,5 % de silicium sont réservés aux transformateurs.

L'augmentation de la perméabilité et la diminution corrélative des pertes par hystérésis sont attribués au fait qu'en présence de silicium, le carbone ne précipite pas sous forme de carbure de fer, mais sous forme de graphite. La diminution de l'anisotropie magnéto cristalline et de la magnétostriction Contribue également à l'accroissement de μ_r. L'amélioration de la stabilité dans le temps est due à la fixation de l'azote sous forme de nitrures Si₃N₄ et à la précipitation du graphite.

On peut augmenter la perméabilité du fer silicié par un procédé permettant d'aligner les axes cristallins de tous les grains (fig. 3.91).



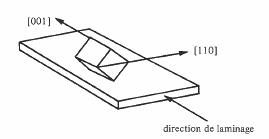
Fig. 3.91 Texture de Goss.

Ce procédé, découvert par Goss, consiste en une succession de laminages à froid et de traitements thermiques appropriés. Les directions d'aimantation facile du fer étant de la forme (100), l'une d'entre elles est parallèle à la direction de laminage. La variation des propriétés magnétiques en fonction de l'angle de H avec la direction de laminage est illustrée à la figure 3.92.



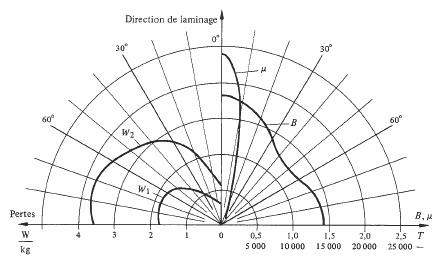
Fig. 3.92 Caractéristiques typiques du Fe-Si orienté (3,5 % Si) d'après [46]. Bande d'épaisseur 0,35 mm ; μ = perméabilité pour B = 1,5 T (continu); B = induction pour H = 800 A/m; W₁ = pertes totale à 50 Hz et B = 1 T; W₂ = pertes totale à 50 Hz et B = 1,5 T.

Les tôles en fer silicié orienté ne sont donc utilisées au maximum de leurs possibilités que lorsque B est partout parallèle à la direction de laminage. Cette condition est parfaitement remplie dans les noyaux en ruban enroulés (fig. 3.78 (b). Dans les noyaux en EI, on se contente généralement de la solution de la figure 3.93, pour les transformateurs de faible puissance. Les noyaux de même forme destinés aux transformateurs de forte puissance sont plus finement divisés, afin de limiter les volumes où B s'écarte de la direction de laminage.



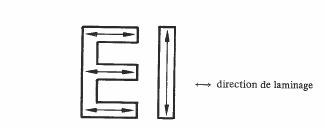
Fig. 3.93

3.9.4 Alliages fer-nickel

On obtient des alliages aux propriétés magnétiques intéressantes avec des pourcentages de nickel dans le fer compris entre 28% et 78%. Par l'adjonction d'une faible quantité d'autres métaux tels que le cuivre, le chrome ou le molybdène, une amélioration significative des caractéristiques est souvent acquise. Les traitements thermiques sous champ magnétique ont également un effet bénéfique. De tous les matériaux disponibles sur une base industrielle, ces alliages possèdent les plus hautes perméabilités et les plus bas champs coercitifs. Leur induction à saturation par contre est peu élevée; dans certains cas, elle ne représente que le tiers de celle d'un fer silicié. Ils possèdent une résistance mécanique qui permet de les travailler facilement. Ils sont relativement onéreux, voire très onéreux selon les nuances, en raison du coût élevé du nickel et de la complexité de certains traitements thermiques.

Les alliages fer-nickel sont des solutions solides. En dessous de 25% de nickel, ils ont la structure du fer (cubique centrée); en dessus, celle du nickel (cubique face centrée). Ils sont disponibles sur le marché à quatre concentrations de nickel différentes.

Les alliages à 30% Ni environ (Thermoflux, R 2799) ont une température de Curie voisine de la température ambiante, et ajustable lors de l'élaboration de l'alliage. Dans une plage de température atteignant 70 C et même davantage, la perméabilité décroît quasi linéairement quand la température augmente, à condition que le champ appliqué H soit suffisamment élevé, par exemple 10⁴ A/m (fig. 3.94).



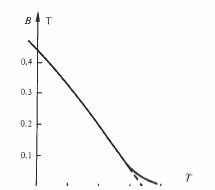
Ces alliages sont utiles, par exemple, pour compenser la dérive thermique dans les électroaimants des appareils de mesure, des compteurs d'électricité, etc.

Les alliages à 36% Ni environ (Anhyster B, Permenorm 3601, Radiometal 36) sont intéressants par leur résistivité électrique élevée. Leur perméabilité est relativement basse, mais pour certaines nuances, elle a la propriété de rester très constante en fonction du champ, dans le domaine de Rayleigh. Leur induction à saturation est assez élevée, pour un alliage fer-nickel. Ils sont utilisés dans la fabrication d'inductances et de translateurs téléphoniques.

Les alliages à 50% Ni environ permettent d'obtenir, par laminage et traitements thermiques appropriés, des matériaux aux qualités magnétiques fort différentes.

Par un recuit prolongé à 1000C, sous hydrogène, on atteint une perméabilité proche de celle des alliages à 75-80% de nickel. Par rapport à ceux-ci, ils possèdent alors l'avantage d'une induction à saturation plus élevée (Anhyster D, Permax M, Permenorm 5000 H2, Radiométal 50).

Par recristallisation après un fortlaminage à froid, on peut obtenir une texture du type représenté à la figure 3.95. Le matériau présentealors un cycle d'hystérésis rectangulaire, et son domaine d'application comprend lesamplificateurs magnétiques, les mémoires, etc.(Permenorm 5000 Z, HCR).

En laminant à froid un ruban présentant cette texture, on peut obtenir un matériau dont la direction d'aimantation facile est perpendiculaire à la direction de laminage. La perméabilité selon la direction de laminage est alors faible, mais très constante en fonction du champ, par exemple : µ_ri = 90, µ_max = 100 (Isoperm).

Les alliages à 75-80% Ni (Mumetal, Permalloy, Permimphy, Ultraperm 10) présentent les perméabilités initiales et maximales les plus élevées et les champs coercitifs les plus faibles. Leur induction à saturation est la plus basse de la série. A ces compositions, l'anisotropie magnéto cristalline est quasi nulle. Il s'ensuit une diminution de l'énergie des parois de Bloch, réduisant les forces d'épinglage exercées par les inclusions. La magnétostriction étant aussi très faible, le déplacement des parois n'est pas gêné non plus par l'apparition de contraintes au niveau des domaines, comme discuté au paragraphe 3.7.7. Ces deux particularités sont à l'origine des hautes perméabilités observées qui trouvent une application dans les domaines suivants : transformateurs de mesure, têtes d'enregistrement, transformateurs haute fréquence, transformateurs d'impulsions, filtres, blindages magnétiques, amplificateurs magnétiques, etc.

3.9.5 Alliages spéciaux

Les alliages au cobalt présentent les plus fortes inductions à saturation et les températures de Curie les plus élevées. Le cobalt est soluble dans le fer jusqu'à une concentration de 75%, la structure est cubique centrée.

Au voisinage de 30% de cobalt, l'alliage peut être moulé, procédé de mise en forme particulièrement adapté à la fabrication de pôles d'aimants.

A 50% de cobalt environ (Permendur), la perméabilité est plus élevée, l'induction à saturation restant proche du maximum (2,43 T). Des propriétés mécaniques satisfaisantes ne sont obtenues que par l'adjonction de 1,5% à 2% de vanadium. Le laminage à chaud et à froid devient ainsi possible. Ce genre d'alliage est utilisé dans les générateurs embarqués à bord d'avions où leur valeur de B_sat permet d'économiser poids et espace. Ils sont également précieux pour la fabrication des membranes d'écouteurs téléphoniques, car ils conservent une perméabilité relative différentielle élevée en présence de champs continus importants.



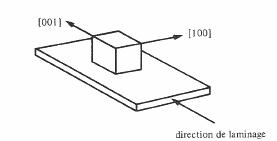
Fig. 3.95

L'alliage à 7 % Co, 70% Ni, 23% Fe (Perminvar) présente une perméabilité très constante en fonction du champ magnétique. De l'ordre de 850, elle ne varie pas de plus d'un pour-cent entre 0 et 0,06 T.

Une concentration d'aluminium dans le fer comprise entre 0 et 16 % donne des alliages dont les propriétés magnétiques sont comparables à celles du fer silicié. Par rapport à ce dernier, ils présentent l'avantage d'une meilleure ductilité. La résistivité croît assez linéairement avec la concentration d'aluminium, et vaut environ 2 fois celle du fer silicié, à 16 % d'aluminium. La perméabilité initiale est en générale plus élevée dans les alliages d'aluminium, tandis que la perméabilité maximum est supérieure dans le fer silicié. L'alliage à 13 % d'aluminium (Alfer) possède une forte magnétostriction. A 16 % d'aluminium (Alperm, Vacodur), la plus haute perméabilité est atteinte. L'usage de ces alliages est limité en raison des dommages coûteux que l'oxyde d'aluminium, formé en surface, inflige aux laminoirs.

Le nickel avec 0,3 % environ de manganèse présente une forte magnétostriction et une résistance élevée à la corrosion. On l'utilise, par exemple, comme transducteur pour l'émission d'ultrasons.

Tout traitement mécanique (déformation), ou thermique (chauffage exagéré) non prévu dans le processus normal d'élaboration, ou dans les conditions d'utilisation peut avoir sur un matériau magnétique des conséquences dramatiques. Les alliages présentant la plus haute perméabilité sont les plus sensibles. A titre d'illustration, la figure 3.96 représente la diminution de perméabilité d'un ruban de Permalloy, provoquée par le simple transfert de ce ruban, d'un tambour de diamètre D₁ sur un tambour de diamètre D₂,



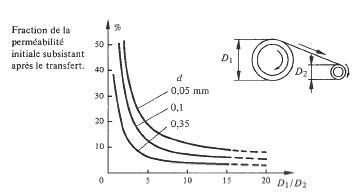
Fig. 3.96 Cas d'un ruban de Permalloy (78% Ni, 4% Mo, 5% Cu, 13% Fe) d'épaisseur d. D'après [45].

3.9.6 Ferrites

Les ferrites sont environ deux fois plus légers que le fer. Ils contiennent 4 ions non magnétiques (oxygène) pour 3 ions magnétiques, dans la structure spinelle. Ces caractéristiques, ainsi que le mécanisme d'alignement des moments magnétiques particulier aux ferrites ( 3.6.3) limitent de manière absolue l'induction à saturation de ces matériaux. Elle est approximativement 5 fois plus faible dans les ferrites que dans les alliages magnétiques.

Par comparaison avec les métaux toujours, la perméabilité initiale et la perméabilité maximum en basse fréquence, sont également plus faibles, parfois de plusieurs ordres de grandeur. Le champ coercitif est plus élevé. Dans un domaine de fréquences qui peut être assez étendu, les pertes magnétiques des moins bons ferrites peuvent être supérieures à celles des rubans magnétiques les plus minces, et surtout à celles des noyaux comprimés. Par contre, la perméabilité des ferrites dépasse le plus souvent très largement celle des noyaux comprimés.

Une résistivité électrique supérieure à celle des alliages magnétiques, dans un rapport pouvant atteindre 14 ordres de grandeur et même davantage est la qualité maîtresse des ferrites, compensant les inconvénients qui viennent d'être énoncés.

Les ferrites et les alliages sont assez dissemblables pour posséder chacun des champs d'application spécifiques. Très schématiquement, le domaine des gros circuits est réservé aux alliages, alors que celui des très hautes fréquences l'est aux ferrites. Il n'y a guère concurrence que pour les composants en électromécanique et en électronique quand les fréquences ne sont pas trop élevées.

Les performances modestes des ferrites en basse fréquence, en termes de _T et H_c ne sont pas imputables à des limitations fondamentales comme dans le cas de B_sat. Elles reflètent les difficultés à obtenir, lors du processus de fabrication, une maîtrise des taux d'impuretés et des structures aussi complète que dans le cas des métaux.

Répertoriés par leur propriétés les plus caractéristiques, les ferrites se divisent en trois classes :

• lesferrites à haute perméabilité ;
• les ferrites à faibles pertes en haute fréquence;
• les ferrites à pertes par résonance (3.9.7).

La famille des ferrites au manganèse Mn_1-x Zn_xFe₂ 0₄ est la plus représentative des ferrites à haute perméabilité. La perméabilité initiale est de l'ordre de 500 à 10 000, selon les nuances. La résistivité est relativement basse en raison de la présence d'ions ferreux dans les sites B. Ces ions libèrent des électrons selon la réaction.

Fe⁺⁺ ⇔  Fe⁺⁺⁺ + e^-                                                       (3.151)

Caractérisée par une faible énergie d'activation. Une certaine concentration d'ion Fe⁺⁺ est par ailleurs nécessaire pour diminuer l'anisotropie magnétocristalline. Il n'est donc pas possible d'obtenir simultanément une haute perméabilité et de faibles pertes par courants de Foucault. En admettant que la fréquence utile maximum est celle où la perméabilité est réduite, par les courants de Foucault, à la moitié de sa valeur en courant continu, les ferrites au manganèse peuvent être employés jusqu'à quelques centaines de kHz.

La famille des ferrites au nickel Ni_1-x Zn_xFe₂ O₄ est la plus représentative des ferrites à faibles pertes en haute fréquence. La présence d'ions ferreux peut être évitée ici, en provoquant un léger déficit en fer par rapport à la valeur théorique de 2 ions par molécule. Il en résulte une résistivité supérieure de plusieurs ordres de grandeur à celle des ferrites au manganèse, rendant dans la plupart des cas les pertes par courants de Foucault totalement négligeables. Les pertes liées à la présence de défauts à l'intérieur des grains sont également faibles, par le fait que les grains sont suffisamment petits pour ne constituer souvent qu'un seul domaine magnétique. La polarisation ne s'établit donc que par rotation et tout mécanisme dissipateur lié au mouvement des parois de Bloch est évité. La perméabilité initiale s'en trouve malheureusement diminuée.

Le procédé de fabrication des ferrites est semblable à celui des céramiques ( 4.10.2) Les figures 3.97 et 3.98 montrent un échantillonnage de noyaux en ferrite.



Fig. 3.97 Série denoyaux pour la confection d'inductances en pots, d'après [47].

3.9.7 Ferrites à pertes par résonance

En plus des pertes étudiées jusqu'ici, qui varient régulièrement avec la fréquence, les matériaux magnétiques présentent des pertes par résonance provoquées principalement par une résonance des spins eux-mêmes.

Un moment magnétique m libre, placé dans un champ continu H, s'anime d'un mouvement de précession. Pour le spin d'un électron libre, la fréquence f_p de précession se déduit de l'équation suivante ([39] chap. 3)

                                                              (3.152)

ν = 35 kHz/Am^-1                                                                        (3.153)

Dans un ferrite où, par exemple, B = 0,5 T, on aurait H = 1/μ_o 0,5 T = 4-10⁵ Am^-1,
d'où f_p = 14 GHz. Ce calcul simple suffit à montrer que la résonance des spins se produit dans le domaine des hyperfréquences.

Le mouvement de précession d'un spin isolé pourrait durer indéfiniment. Il n'en est pas de même si ce spin est celui d'un électron appartenant à un atome faisant partie d'un cristal, car l'interaction spin-réseau cristallin exerce un effet d'amortissement sur le mouvement de précession. Ce mouvement cesse donc après un nombre plus ou moins grand de révolutions, mais de toute façon après un temps très court. Le transfert d'énergie du spin au réseau accompagnant ce processus est à l'origine des pertes par résonance.

Le schéma d'un dispositif exploitant ces pertes est donné à la figure 3.99.



Fig. 3.99

L'aimant permanent aligne dans le ferrite les axes de précession. Quand la fréquence de l'onde incidente est égale à la fréquence de précession des spins, l'onde transfère la plus grande part possible de son énergie à l'ensemble des spins, qui la cèdent à leur tour au réseau cristallin dans lequel elle prend la forme calorifique.

Le mouvement de précession forcée des spins peut être uniforme, mais il peut exister aussi des ondes de spin. Ces dernières sont formées par une variation spatiale progressive de l'orientation des spins (fig. 3.100).

Ces ondes se propagent dans le ferrite, ou forment au contraire un système d'ondes stationnaires. Un grand nombre de composants utilisés en hyperfréquence, dans des circuits à faible ou forte puissance, utilisent plus ou moins le principe présenté à la figure 3.99. On peut citer par exemple les circulateurs, les isolateurs, les déphaseurs, etc.



Fig. 3.100 Représentation schématique d'une onde de spin. H est dirigé selon z. m_s = moment magnétique dû au spin.

Dans les alliages et les ferrites à relativement basse résistivité, la pénétration d'une onde hyperfréquence est extrêmement limitée, et la résonance des spins n'est pas une propriété exploitable.

Les ferrites à haute résistivité les plus intéressants en hyperfréquence possèdent la structure du grenat, ou la structure spinelle.

Les ferrites au nickel sont indiqués où une polarisation magnétique importante est nécessaire, leur résonance est large. Ils ont l'inconvénient de présenter des pertes magnétiques et diélectriques relativement élevées, et d'être sensibles aux contraintes mécaniques.

Les ferrites au lithium sont plus stables en présence de sollicitations mécaniques et thermiques, car leur température de Curie est plus élevée. Dans un grand nombre de situations, ils représentent le meilleur choix possible, exception faite des cas où l'influence des pertes diélectriques est déterminante.

Sur ce point les ferrites à structure de grenat sont nettement supérieurs, car ils ne renferment pas d'ions ferreux si le dosage est correct. Leur résonance est étroite. Le matériau le plus courant est le grenat d'yttrium et fer (YIG).

La largeur du domaine de la résonance ne dépend pas seulement de la composition, mais encore d'autres facteurs tels que la forme de l'échantillon, son état de surface, le champ appliquera microstructure (dimension et orientation des grains), les traitements thermiques, etc.. L'effet du champ appliqué est illustré à la figure 3.101, pour le cas d'un ferrite NiZnFe₂O₄. Les pertes sont exprimées par la composante imaginaire de la perméabilité m_r" (3.133).



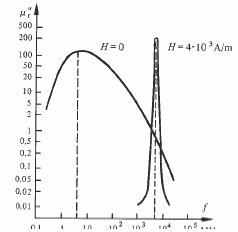
Fig. 3.101 D'après [45].

La variation de la fréquence de résonance en fonction de H est linéaire, comme en témoigne la figure 3.102. Le même comportement était prévu pour des spins libres,par l'équation (3.152). De plus, la pente de la droite est très voisine de la valeur de v.
Une bibliographie importante sur les propriétés et les applications des ferrites en hyperfréquences est reportée à la fin de [37] qui constitue une synthèse sur le sujet.



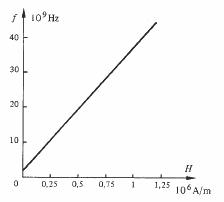
Fig. 3.102 /p (H) dans un échantillon polycristallin sphérique de ferrite N;Fe₂ O₄, d'après [34].

3.9.8 Noyaux comprimés

Les noyaux comprimés sont constitués d'une poudre de fer, ou d'alliage fer-nickel, dont le diamètre des grains est de l'ordre de 50 um à 100 (im. Ces grains, enrobés d'un isolant, sont comprimés en présence d'un liant adéquat pour obtenir le noyau, généralement de forme torodale. La fine division du matériau magnétique réduit fortement les pertes par courants de Foucault, ce qui rend les noyaux comprimés utilisables jusqu'à quelques centaines de kHz. Il faut toutefois remarquer que ce résultat n'est obtenu qu'au prix d'un sacrifice important touchant la perméabilité, dont la valeur est généralement comprise entre 10 et 100. L'isolation de chaque grain constitue un entrefer.
L'effet cumulé de ces entrefers explique que la perméabilité du noyau soit de plusieurs ordres de grandeur inférieure à celle des grains eux-mêmes. L'usage des noyaux comprimés est en voie de disparition, ils sont remplacés par les ferrites.

3.10   MATÉRIAUX MAGNÉTIQUES DURS

3.10.1  Introduction

La seule application des matériaux magnétiques durs réside dans la fabrication des aimants permanents. L'usage de ces aimants est très répandu et touche par exemple les domaines suivants : moteurs, générateurs et autres machines tournantes, écouteurs téléphoniques et haut-parleurs, instruments de mesure, composants hyperfréquence, supports d'enregistrement : bandes et disques magnétiques. L'industrie des biens de consommation en absorbe également une quantité importante. Dans son ensemble, le marché des matériaux magnétiques durs égale ou même surpasse légèrement, financièrement parlant, le marché des matériaux magnétique doux.

L'unique fonction d'un aimant permanent est de créer un champ magnétique extérieur. Cela implique que l'aimant possède des pôles, qui sont les régions dans lesquelles sa polarisation I présente une composante normale à la surface. L'intensité des pôles se mesure par la densité superficielle des masses magnétiques a_m (3.85) qui y sont accumulées. Ces masses provoquent un champ démagnétisant H_d (sect. 3.7.5).

Un échantillon de matériau magnétique dur ne devient un aimant permanent, qu'après avoir subi l'action d'un champ magnétique H_mag destiné à provoquer, au niveau des domaines, les modifications irréversibles de la polarisation amenant l'apparition des pôles. Dans le diagramme B-H (fig. 3.103) cette opération correspond au trajet O.S.P.



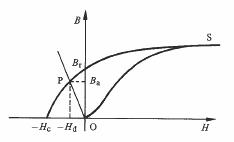
Fig. 3.103

Le champ démagnétisant, inexistant au départ, se crée progressivement et se stabilise à la valeur H_d lorsque H_mag revient à zéro. La présence des pôles réduit donc, par H_ä, l'induction dans l'aimant à une valeur B_a, inférieure à B_r. Rappelons que B_r, valeur spécifique du matériau, est déterminée sur un échantillon ne présentant pas de pôles (forme torique).

La droite OP est appelée droite de charge ( IX.3.2.5), et la portion du cycle principal pour laquelle B > 0 et H < 0, caractéristique de désaimantation. La pente de la droite de charge variant en fonction de la forme de l'aimant et de l'occupation de son entrefer, la connaissance complète de la caractéristique de désaimantation est nécessaire
pour le calcul des aimants (chap. IX.3).

Le maximum du produit BH sur la caractéristique de désaimantation est une donnée importante. En effet, le meilleur usage du matériau magnétique est obtenu en régime statique quand l'aimant travaille à BH maximum.

3.10.2 Alnico, Ticonal

Les alliages les plus largement utilisés comme matériaux magnétiques durs comportent en plus du fer, du cobalt et du nickel, puis, dans des proportions plus restreintes, de l'aluminium et du cuivre, parfois d'autres éléments encore. Connus sous les appellations générales Alnico ou Ticonal, ces matériaux portent encore un grand nombre de marques de fabrique différentes. Dans la suite, on les désignera simplement par Alnico.

Les Alnicos sont très durs et cassants, de sorte que la mise en forme se fait à la fabrication même de l'alliage par coulée ou frittage. Le premier procédé donne des grains très gros, de l'ordre de 1 mm de diamètre, le second des grains beaucoup plus petits.

La dureté magnétique des Alnicos est obtenue par un traitement thermique qui leur confère une structure particulière. L'alliage est tout d'abord chauffé à '250C jusqu'à l'obtention d'une solution solide homogène, appelée phase α. Au cours d'un refroidissement, effectué à la vitesse de 1 C par seconde environ jusqu'à une température inférieure à 500C, apparaît une seconde phase α', enrichie en fer et cobalt, et très magnétique. Pendant un recuit à 600C, α' s'enrichit encore en fer et cobalt au détriment de α à tel point que α pourra même devenir paramagnétique. Finalement, α' se présente sous la forme de petits cylindres allongés d'un diamètre de 30 nm et d'une hauteur de 120 nm environ alignés sur la direction 〈100〉 de α. La dimension réduite de ces cylindres fait qu'ils ne peuvent contenir qu'un seul domaine magnétique. Leur forme allongée leur confère une très haute énergie magnétostatique ( 3.7.5), qui lie fortement la direction de polarisation à l'axe des cylindres. La dureté des Alnicos tire donc son origine de la forme des particules mono-domaine qui les constituent.

Un échantillon polycristallin ayant subi le traitement qui vient d'être décrit sera, à l'échelle macroscopique, magnétiquement isotrope. Cela présente rarement un avantage. Par contre, en produisant une anisotropie il serait possible d'augmenter B_T et H_c. Dans ce but, on peut appliquer un champ magnétique pendant la formation du précipité. Le développement des cylindres dont l'axe concide avec la direction <100> la plus proche du champ est alors favorisé, car cette disposition minimise l'énergie magnétostatique (en présence du champ). L'anisotropie magnétique est encore accentuée si l'on a provoqué, en contrôlant la solidification de l'alliage, une structure dans laquelle les axes des grains sont orientés préférenciellement dans la direction de polarisation. Les améliorations obtenues apparaissent dans la figure 3.104.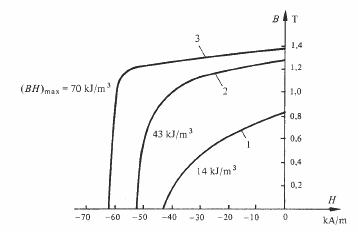


Fig. 3.104 D'après [48] : 1, Alnico à structure granulaire isotrope, recuit sans champ magnétique; 2, Alnico à structure granulaire isotrope, recuit sous champ magnétique; 3, Alnico à structure granulaire orientée, recuit sous champ magnétique.

3.10.3 Ferrites

Par leur structure hexagonale, les ferrites au baryum, et au strontium ( 3.6.7) présentent une forte anisotropie cristalline, qui en fait des matériaux magnétiques durs aux propiétés intéressantes. Leur caractéristique de désaimantation se dif férencie nettement de celle des Alnicos, par un champ coercitif plus élevé et une induction rémanente plus basse (fig. 3.105).



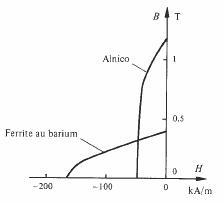
Fig. 3.105

La meilleure utilisation des ferrites est donc obtenue dans les aimants de forme aplatie, polarisés dans le sens de l'épaisseur. Les ferrites supportent bien le grand facteur démagnétisant de cette géométrie, qui présente par ailleurs l'avantage de compenser leur relativement faible rémanence en offrant une importante section au passage de B. Par comparaison, les aimants en Alnicos doivent avoir une forme allongée.

Les ferrites sont plus légers et passablement moins chers que les Alnicos, ils permettent la fabrication d'aimants souples par la dispersion de poudre de ferrite dans des substances telles que les thermoplastiques ou les élastomères.

3.10.4 Autres matériaux

Par les quantités utilisées, les Alnicos et les ferrites viennent nettement en tête. Il existe néanmoins, un grand nombre d'autres matériaux magnétiques durs, dont l'importance est parfois décisive pour certaines applications.

Les composés de terres rares, répondant à l'une des formules générales RM, RM₂, RM₅ et R₂M₁₇ font l'objet de recherches intenses en raison de leurs anisotropies magnétocristallines extraordinaires élevées, de l'ordre de 20 fois supérieures à celle du ferrite au baryum par exemple. R désigne une terre rare, ou l'yttrium, et M un métal de transition. Le composé le plus intéressant sur le plan pratique est actuellement le SmCo₅ (tab. 3.109). Sa structure est hexagonale comme celle de tous les composés RM5. Son prix demeure relativement élevé en raison du coût de raffinage du samarium. (La grande similitude chimique des terres rares rend difficile leur séparation). Avec la formule R₂ M₁₇ il est possible d'utiliser pour R₂ un mélange naturel de terres rares, à prédominance de cérium, ce qui pourrait faire baisser le coût des aimants aux terres rares.

La technique des poudres comprimées est également utilisée pour fabriquer des aimants selon le processus suivant. Des particules allongées de Fe-Co sont déposées par voie électrolytique sur un bain de mercure. Leurs dimensions sont telles qu'elles ne contiennent qu'un seul domaine magnétique. Du plomb est ajouté, qui forme un amalgame. Le mercure est ensuite évaporé. La fine couche de plomb restant sur les particules sert de liant lors de la mise en forme de la poudre par pressage. (Il n'est pas nécessaire ici que les grains soient isolés électriquement les uns des autres). Selon qu'on désire un matériau anisotrope ou isotrope, la mise en forme se fera sous champ magnétique ou non. La structure obtenue, formée de grains magnétiques allongés, disposés dans une matrice non magnétique est semblable à celle des Alnicos, avec cet avantage que les dimensions et proportions des grains peuvent être variés beaucoup plus facilement, pour obtenir des caractéristiques particulières. La technique des poudres est très adaptée à la fabrication d'aimants aux formes compliquées et requérant une grande précision mécanique, car la mise en forme de la poudre est l'opération finale, il n'y a pas de recuit ni surtout de frittage entraînant des retraits plus ou moins bien contrôlés. Ces aimants équipent par exemple les micromoteurs, les instruments de mesure, etc.

Les aciers trempés à haute teneur en carbone dont on a fait toutes les aiguilles de boussoles pendant des siècles ne sont plus guère utilisés. Leur prix serait bas mais leurs performances sont aujourd'hui jugées insuffisantes, sauf dans le cas de l'acier contenant 3,5 % de chrome. La dureté magnétique de ces matériaux est due à la présence d'inclusions et de microcontraintes freinant le déplacement des parois de Bloch.

Signalons pour terminer qu'il existe des alliages faisant exception à la règle selon laquelle les matériaux durs magnétiquement, le sont aussi mécaniquement. Le plus célèbre d'entre eux est certainement l'alliage CoPt, le matériau magnétique le plus cher jamais produit à l'échelle industrielle, pour son H_c élevé, et remplacé aujourd'hui par les composés de terres rares.

3.10.5 Matériaux pour l'enregistrement magnétique

Le support des enregistrements magnétiques est constitué d'une fine couche d'oxyde magnétique disposé dans un liant plastique adéquat, et déposé sur une bande ou un disque.

Un oxyde de fer, la maghémite, est utilisé très couramment. Son champ coercitif est bien adapté aux exigences de l'enregistrement, c'est à dire relativement bas (~ 20 - 25 kA/m). Sa stabilité chimique est excellente et son coût faible. Il ne comporte que des ions trivalents et possède la structure spinelle de Fe₃ O₄, dans laquelle un sixième des sites B reste vacant. Il se présente sous la forme de particules allongées de 0,1 microns de diamètre et 0,6 microns de longueur environ, ne contenant qu'un seul domaine magnétique. La dureté magnétique provient donc de l'énergie magnétostatique développée par la forme des domaines. Lors de la fabrication d'une bande magnétique, on aligne au moyen d'un champ les particules de façon à ce que leur grand axe soit parallèle au sens de défilement de la bande. C'est ainsi que l'induction rémanente maximum est atteinte, car la tête d'enregistrement polarise la bande dans son sens de défilement.

     Le dioxyde de chrome CrO₂ cristallise dans la structure du rutile (TiO₂) et se présente également sous forme de grains allongés. C'est un concurrent de la maghémite, avec un champ coercitif légèrement plus élevé.