Bande

2.6  MODÈLE DES BANDES D'ÉNERGIE

2.6.1 Introduction

Le modèle de Sommerfeld donne une représentation satisfaisante de la plupart des propriétés électroniques des métaux, on vient d'en voir quelques exemples dans la section précédente. Cette constatation justifie a posteriori l'hypothèse de ce modèle selon laquelle les électrons se déplacent librement; c'est-à-dire qu'ils sont soumis, dans la matière, à un potentiel constant. Il est bien connu pourtant, par les expériences de diffraction de rayons X en particulier, que les métaux ont une structure cristalline. Les électrons devraient donc être soumis à un potentiel périodique, dont la période serait liée aux dimensions de la maille du réseau. Il faut en conclure que cette variation périodique de potentiel est faible dans les métaux, et qu'on peut la négliger.

Le cas des semiconducteurs et des isolants est totalement différent. Une conductivité électrique faible, voire quasi nulle, signifie que les électrons de valence restent très fortement liés aux atomes. Cette situation est typique des liens de covalence et de valence ionique, par opposition aux liens de valence métallique (sect. 1.3). Il n'est pas étonnant que le modèle de l'électron libre dans un puits de potentiel échoue complètement dans ce cas.

L'étude des propriétés électroniques des semiconducteurs et des isolants commence donc par l'analyse du comportement d'un électron dans un potentiel périodique.
Il est difficile d'aborder ce problème de front, dans l'espace à 3 dimensions. Heureusement les résultats indispensables peuvent être obtenus plus simplement, en considérant un cristal unidimensionnel. Les conclusions pour le cas tridimensionnel seront tirées de manière qualitative seulement.

L'ensemble des développements qui vont suivre constitue les bases élémentaires du modèle des bandes d'énergie et ses premières conséquences. Il n'est pas besoin d'insister sur l'importance de ce modèle qui est à l'origine, entre autres, de toutes les réalisations basées sur l'électronique de l'état solide : diodes, transistors, circuits intégrés. Le nom de ce modèle dérive de son mérite principal, qui est de montrer que les énergies possibles des électrons dans un milieu cristallin sont groupées dans un certain nombre de bandes d'énergies permises, séparées les unes des autres par des bandes d'énergies interdites. A partir de là, un traitement unifié des métaux, semiconducteurs et isolants est possible. La position de l'énergie de Fermi dans la succession des bandes permises et interdites en est le paramètre clé.

2.6.2 Electrons dans un potentiel périodique. Cas unidimensionnel

L'énergie potentielle W_pot d'un électron dans un cristal unidimensionnel de vecteur fondamental a possède l'allure décrite à la figure 2.21. Le comportement de cet électron est régi par l'équation de Schrödinger, qui prend ici la forme :

             (2.101)

Cette équation admet pour solutions des fonctions du type

              (2.102)

      

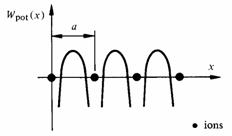
Fig. 2.21

appelées fonction de Bloch. La fonction U_k(x) est périodique, de même période a que le cristal :

U_k (x+a) = U_k (x)             (2.103)

U_k(x) dépend de la forme choisie pour W_pot(x). Toutes les formes raisonnables de W_pot(x) conduisent cependant à des résultats comparables. On prendra pour W_pot(x) l'approximation du modèle de Kronig et Penney. Cette approximation est très schématique (fig. 2.22), mais elle conserve les caractéristiques principales du potentiel réel: même périodicité que le réseau, maximum de potentiel entre les ions, minimum au voisinage des ions.

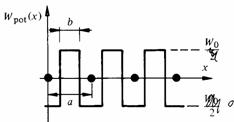
Fig. 2.22 Potentiel périodique admis dans le modèle de Kronig et Penney. On notera que le minimum de l'énergie est fixé à zéro, de manière à pouvoir effectuer un passage à la limite de la hauteur de potentielle, sans toucher les 2 extrêmes en même temps.

Le paramètre b, largeur de la barrière de potentiel séparant deux ions voisins, permettra d'étudier l'incidence sur le résultat d'une liaison plus ou moins forte des électrons avec les atomes.

L'intégration de (2.101) avec pour W_pot (x) la fonction représentée à la figure 2.22 est en principe simple, toutefois les calculs sont assez fastidieux. On se contentera d'en décrire ici le déroulement. L'équation (2.101) est tout d'abord résolue séparément pour les régions où W_pot(x) = + W₀  et W_pot (x) = 0. Les fonctions d'onde trouvées, ainsi que leurs dérivées en fonction de x sont ensuite couplées (condition de continuité) aux frontières des domaines dans lesquels l'énergie potentielle est constante. On obtient de la sorte une équation aux valeurs propres, dont la forme se simplifie considérablement dans le cas où la barrière de potentiel séparant deux ions prend l'allure d'une fonction de Dirac, W_o tendant vers l'infini alors que W_o b reste constant. Dans ces conditions il vient :

             (2.104)

où
           (2.105)

          (2.106)

La signification de (2.104) apparaît clairement lorsqu'on représente graphiquement (fig.2.23) le membre de droite de cette équation, en fonction de a.

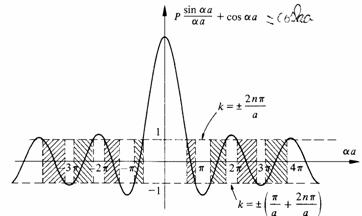
Fig. 2.23

Seules les portions de cette fonction comprises entre les deux horizontales à 1 doivent être retenues comme solutions de (2.104), en raison du cosinus dans le membre de gauche. L'axe a présente donc une alternance de segments à l'intérieur desquels (2.104) tour à tour possède ou ne possède pas de solutions ayant un sens physique.

Les énergies possibles d'un électron soumis à un potentiel périodique sont donc confinées dans ce qu'il est convenu d'appeler des bandes d'énergies permises, séparées les unes des autres par des bandes d'énergies interdites.

2.6.3 Cas limites

La largeur des bandes permises dépend de la hauteur de la barrière de potentiel séparant deux ions. Plus cette barrière est haute (W_o b important), plus l'amplitude de la fonction oscillante de la figure 2.23 est grande, ce qui entraîne une diminution de la largeur des bandes permises. A la limite, pour W_o b tendant vers l'infini, l'équation (2.104) se réduit à

 

         sin α a = 0                 (2.107)

d'où

          α a = n            avec n = 1, 2, 3, ..               (2.108)

et, par (2.106)

                                        (2.109)

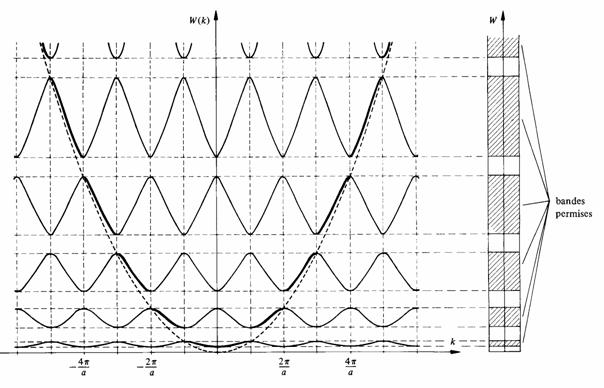
Fig. 2.24

On retrouve les énergies permises (2.54) pour un électron libre dans un puits de potentiel de largeur a. La largeur des bandes permises s'est réduite jusqu'à devenir infiniment petite. Réciproquement, si l'on abaisse la barrière de potentiel jusqu'à zéro, (2.104) devient :

cos k a = cos α a                         (2.110)

II n'y a plus aucune limitation sur les énergies possibles de l'électron, il est totalement libre ou, ce qui revient au même, confiné dans un puits de dimension infinie.

Ces deux cas extrêmes montrent la souplesse du modèle qui permet de traiter aussi bien des électrons de valence quasi libres, que des électrons de couches plus profondes liés fortement au noyau.

2.6.4 Fonctions W(k)

II est utile pour la suite d'examiner l'équation (2.104) sous un autre angle, et en particulier d'étudier les fonctions W(k) à l'intérieur des bandes permises. Dans la figure 2.23, l'horizontale supérieure correspond aux valeurs de k suivantes :

              (2.111)

L'horizontale inférieure correspond à :

       (2.112)

En restant à l'intérieur d'une même bande permise, lorsque k croit ou décroit continûment, on décrit de façon alternative le tronçon correspondant de la fonction P sin ( a ) / a + cos ( a ). La variation concommitante de a montre que dans chaque bande permise, l'énergie de l'électron est une fonction paire de k. La période vaut 2 /a. Les fonctions W (k) ont donc l'allure représentée à la figure 2.24.

Pour comparaison, on a reporté sur la figure 2.24 la parabole W(k) du modèle de Sommerfeld (2.54) et marqué en trait plus épais les portions des fonctions W(k) du modèle des bandes proches de cette parabole. On constate que le remplacement du potentiel constant par un potentiel périodique correspond à une déformation de la parabole, dont la caractéristique la plus importante est la succession de brisures apparaissant aux abscisses multiples de  /a. Ces brisures correspondent aux bandes interdites.

La parabole de Sommerfeld n'était en fait pas une fonction continue, mais une succession de points représentatifs d'états discrets. Selon le paragraphe 2.6.2, toute énergie comprise dans une bande permise serait possible. En réalité ce n'est pas le cas, ce résultat tient à ce que le cristal unidimensionnel a été implicitement supposé infiniment long. En réduisant ce cristal à une dimension finie, il apparaît que chaque bande est aussi formée d'une succession d'états discrets proches les uns des autres.

2.6.5 Nombre d'états dans une bande

Le nombre d'états énergétiques dans une bande permise dépend de la taille du cristal. Considérons le cristal unidimensionnel représenté à la figure 2.25. Il possède N atomes, sa longueur L et son vecteur fondamental a.

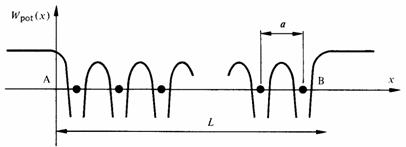
Fig. 2.25  Energie potentielle d'un électron dans un cristal linéaire fini.

Le nombre d'états recherché s'obtiendrait, en principe, en résolvant l'équation 2.101, avec l'énergie potentielle de la figure 2.25. Toutefois, même en idéalisant fortement W_pot(x) comme on l'a fait pour le cristal infini, les développements mathématiques seraient très laborieux. Une façon élégante de se tirer d'affaire est de recourir aux conditions cycliques de Born, basées sur l'observation suivante :

Un cristal comporte toujours un très grand nombre d'atomes. L'influence de la forme exacte des barrières de potentiel aux limites du cristal a donc peu d'influence sur l'énergie des électrons. Il suffit que ces barrières empêchent les électrons de quitter le cristal. On peut donc choisir leur forme de manière à simplifier au maximum les calculs.

Dans ce but, imaginons que l'on courbe le cristal jusqu'à mettre son extrémité A en contact avec son extrémité B (à l'échelle atomique, cette opération ne s'accompagne que d'une infime déformation en raison du rapport énorme entre le rayon de courbure et le vecteur fondamental du cristal). On redonne ainsi à la fonction d'onde dans un cristal fini, le caractère périodique qu'elle avait dans un cristal infini :

          Ψ (x + L) = Ψ (x)           (2.113)

Cette équation exprime la condition cyclique de Born. En imposant (2.113) à la solution générale (2.102) il vient:

U_k (x + L) exp[ j k (x+L)] = U_k (x) exp (j k x)             (2.114)

Or, U_k est périodique de période a, et L = Na             (2.115)

(2.114) entraîne donc k L= 2  l            (2.116)

l étant un entier quelconque.

Aux deux extrémités d'une bande (fig. 2.24), k prend les valeurs limites

                   (2.117)

         (2.118)

Le nombre N_e de valeurs possibles de k entre ces deux limites correspond au nombre d'états énergétiques possibles dans la bande. Comme k varie par pas de 2 n/L, ainsi que le montre l'équation (2.116), il vient :

                   (2.119)

Ce résultat doit être multiplié une première fois par 2 pour tenir compte du spin, puis une seconde fois par 2 car on a négligé les valeurs négatives de k. Finalement:

 

          N_e = 2N                   (2.120)

 

Le nombre d'états dans une bande est donc proportionnel au nombre d'atomes dans le cristal. Ce résultat est important, car il montre qu'il y a toujours assez de places pour loger les électrons d'un cristal de nature donnée, quelle que soit sa taille, sans enfreindre le principe de Pauli ou recourir à des bandes d'énergies supérieures.

2.6.6 Masse effective de l'électron. Définition

Le calcul de la réponse d'un électron à un champ extérieur n'est pas immédiat, dès le moment où cet électron n'est plus libre, mais soumis au potentiel créé par les ions d'un cristal. La nature d'un problème clé comme celui de la détermination d'une densité de courant change fondamentalement même si, finalement, un formalisme identique à celui adopté dans le modèle Boules de billard peut être établi.

Si l'on considère l'électron comme une particule classique, l'équation de Newton est applicable :

 

        F = m_n a                  (2.121)

La force F agissant sur l'électron a deux composantes :

       F = F_int + F_ext          (2.122)

F_ext est la force due au champ extérieur, F_int la force dérivant du potentiel créé par les ions. La forme de (2.121) est très simple mais son usage pour calculera reste problématique car F_lnt n'est pas connu.

Cette difficulté est résolue par l'introduction d'une masse effective de l'électron m_n∗, définie par la relation suivante :

          (2.123)

L'intérêt du procédé réside évidemment dans le fait que m∗ peut être calculée facilement.

2.6.7 Calcul de la masse effective de l'électron

Pour déterminer m_n∗ il faut recourir simultanément aux résultats de la physique classique et à ceux de la physique quantique. L'articulation entre les deux théories se fait au moment où l'on admet qu'il y a un électron, considéré comme une particule classique, à l'endroit où (x )² présente un maximum, c'est-à-dire au centre du paquet d'ondes. La vitesse de l'électron est donc égale à la vitesse de groupe v_g de l'onde qui le représente.

Il est bien connu par la théorie des ondes que

                   (2.124)

où w est la pulsation de l'onde. Le vecteur d'onde k se réduit dans un modèle unidimensionnel au nombre d'onde k déjà rencontré. D'autre part, w ne dépend ici que de k. On utilisera donc (2.124) sous la forme

                 (2.125)

L'énergie de l'électron est liée à la pulsation de l'onde par la relation d'Einstein : 

                              (2.126)

qui permet d'écrire (2.125) sous la forme :

                (2.127)

En dérivant (2.127) par rapport au temps on obtient l'accélération de groupe a_g qui n'est rien d'autre que le module de l'accélération figurant dans le membre de droite de (2.123). Il vient:

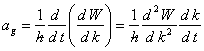               (2.128)

II reste à faire apparaître F_ext dans (2.128) pour être à même de comparer cette équation à (2.123) et d'en tirer m_n∗. Ecrivons le travail de F_ext sur l'électron :

F_ext v_g dt = dW          (2.129)

d'où

             (2.130)

Par (2.127):

        (2.131)

En portant (2.131) dans (2.128) il vient, après identification de l'expression obtenue avec la relation (2.123) :

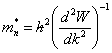          (2.132)

La masse effective de l'électron dépend donc de son énergie par l'intermédiaire d'une dérivée de la fonction W (k) représentée à la figure 2.24.

2.6.8 Commentaires sur la masse effective de l'électron

Dans le modèle de Sommerfeld, l'énergie de l'électron est liée au nombre d'onde par (2.54). On tire de cette équation

              (2.133)

D'où par (3.132)

                     m_n = m_n^∗                       (2.134)

 

Ce résultat est cohérent avec le fait que l'électron n'est pas considéré, dans ce modèle, comme soumis au potentiel périodique des ions.

Dans le modèle des bandes les conclusions sont plus intéressantes. Considérons la bande d'énergie la plus basse et les plus faibles valeurs de k (tab. 2.26). Des résultats semblables seraient obtenus avec n'importe quelle bande permise et n'importe quel intervalle de k.

 

Tableau 2.26 Déduction qualitative de la variation de la masse effective d'un électron en fonction de son énergie

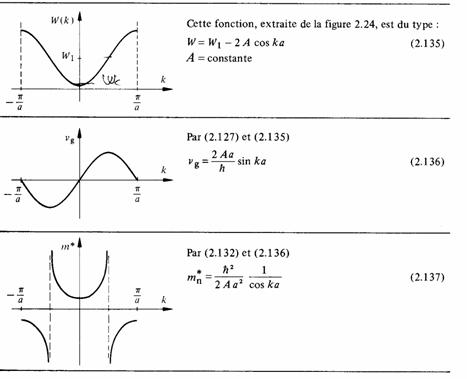
augmente, elle devient infinie au milieu de la bande. Dans cette situation une force extérieure ne peut plus communiquer d'accélération à l'électron. Plus haut dans la bande, la masse effective devient négative! Cela doit nous rappeler que la masse effective n'est qu'un paramètre, possédant la dimension d'une masse, et calculé pour que (2.123) s'applique. Ce n'est donc pas une quantité de matière qui ne saurait évidemment être négative. Quand m∗ < 0, l'accélération est opposée à la force extérieure. Les conséquences en sont examinées dans les paragraphes suivants.

2.6.9 Contribution à la conduction d'une bande totalement occupée

Soit B₁ la bande d'énergies permises dont tous les états sont effectivement occupés par des électrons. Soit B₂ la bande des énergies permises voisine de B₁dans la direction des énergies croissantes. Par hypothèse, B₂ ne contient pas d'électrons. Soit encore B₁ la bande interdite séparant B₁ et B₂.

La bande B₁ ne fournit aucune contribution à la conduction. En d'autres termes, l'application d'un champ électrique E est sans effet sur les électrons de B₁, pour deux raisons :

     1) B₁ ne possède pas, par hypothèse, de niveaux vacants pour accueillir les électrons qui auraient été accélérés par E. Les électrons de B₁ ne peuvent donc subir aucune accélération.

     2) La largeur de la bande interdite est trop importante (sauf exceptions) pour qu'un transfert d'électrons de B₁ dans B₂, à travers B_interdite puisse se produire sous l'action du champ électrique uniquement.

Le fait que les électrons de B₁ ne fournissent aucune contribution à la conduction ne signifie nullement que ces électrons sont immobiles. Chacun d'eux possède au contraire une vitesse n_g donnée par (2.127). Cette vitesse dépend de la position de l'électron dans B₁, ainsi que le montre le tableau 2.26. La bande B₁ étant totalement occupée, il correspond à chaque électron de vitesse + v_g (valeur positive de k), un électron de vitesse - v_g (valeur négative de k), de sorte qu'il ne peut y avoir, dans cette situation, aucun déplacement net de charges dû aux électrons de B₁.

On peut écrire par conséquent :

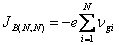             (2.138)

Dans cette expression, J_{B (N1,N2)} représente la contribution à la conduction d'une bande B₁ possédant N₁ états permis dont N₂ sont effectivement occupés par des électrons. L'indice i identifie les électrons, et v_gi représente la vitesse de chacun d'eux.

2.6.10 Contribution à la conduction d'une bande presque totalement occupée

Considérons le cas où un petit nombre d'états de B₁ sont vacants. Ces états sont naturellement situés au sommet de Bi, c'est-à-dire dans la région des énergies les plus élevées.

La présence d'états vacants permet aux électrons de B₁ d'être accélérés et de participer ainsi, d'une certaine manière, à la conduction.

Supposons que seul l'électron No j manque. La contribution de B₁ à la conduction s'écrira:

             (2.139)

ou encore,

            (2.140)

Compte tenu de (2.138)

             (2.141)

L'équation (2.141) montre que la conduction résultant des mouvements des N- 1 électrons de B₁ est équivalente à celle d'une seule particule, portant une charge + e.

S'il manque non pas 1 mais l électrons au sommet de B₁, l restant très petit par rapport au nombre total d'états dans B₁, il vient:

                  (2.142)

2.6.11 Notion de trou.Définition

En résumé, le paragraphe précédent montre que l'absence de l électrons au sommet d'une bande d'énergie est équivalente, du point de vue de la conduction, à la présence de l particules mobiles portant une charge + e.

On appelle ces particules des trous. Un trou peut être considéré comme une particule ordinaire, jouant un rôle comparable à celui de l'électron dans le modèle Boules de billard par exemple. La masse effective du trou est égale à la valeur absolue de la masse effective relative à l'état vacant correspondant.

Le concept de trou est extrêmement utile, en particulier dans l'étude des dispositifs à semiconducteurs (vol. VII). On en verra quelques applications dans cette section également.

Il ne faut pas oublier totalement (ce qu'on est tenté de faire rapidement!) que le trou est une particule fictive. C'est un modèle permettant de rendre compte, de manière très simple mais valable, de la part de conduction relevant des électrons d'une bande presque totalement occupée.

2.6.12 Structure de bandes dans les conducteurs, les semiconducteurs et les isolants.
Définitions

Une question primordiale n'a pas encore été abordée, celle de savoir où se place, dans la succession des bandes permises et interdites, l'énergie de Fermi. Deux cas sont possibles:

• • l'énergie de Fermi est comprise dans une bande permise (fig. 2.27), et l'on a affaire à un conducteur métallique. La bande contenant W_F est appelée bande de conduction, la bande voisine de celle-ci, du côté des énergies décroissantes s'appelle bande de valence;
• • l'énergie de Fermi est située dans une bande interdite et l'on a affaire à un isolant ou à un semiconducteur (fig. 2.28). Ici, la bande de valence est la première bande située au-dessous de W_F, alors que la bande de conduction (vide ou peu occupée) est située immédiatement au-dessus de W_F.

Les deux structures de bandes qui viennent d'être mentionnées sont les seules possibles dans un cristal unidimensionnel. Un autre type de structure peut apparaître dans les cristaux réels ( 2.6.15).

2.6.13 Structure de bandes et résistivité des métaux en fonction de la température

II est bien connu que la résistivité des métaux augmente avec la température. La structure des bandes représentée à la figure 2.27 explique qualitativement ce fait expérimental.

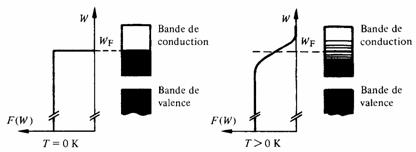
Fig. 2.27 Position de l'énergie de Fermi dans un métal. Les états occupés sont représentés en noir.

A 0 K, tous les niveaux situés en-dessous de W_F, sont occupés, tous les niveaux au-dessus de W_F  sont vacants. Quand la température augmente, l'énergie thermique permet à un certain nombre d'électrons d'acquérir une énergie supérieure à W_F.

Supposons que W_F est au milieu de la bande de conduction. Les électrons transférés à W > W_F, non seulement ne fournissent plus la contribution à la conduction qui était la leur lorsqu'ils avaient une énergie inférieure à W_F, mais encore ils s'opposent au courant créé par les électrons dont W < W_F. En effet, leur masse effective étant devenue négative (tab. 2.26) ils se déplacent en sens inverse des électrons situés en dessous de l'énergie de Fermi. Pour un champ donné, le courant a donc diminué, et par conséquent la résistivité a augmenté.

La variation de la masse effective représentée au tableau 2.26 permet, par un raisonnement analogue au précédent, d'aboutir aux mêmes conditions lorsque W_F  n'occupe pas exactement le milieu de la bande de conduction.

2.6.14 Structure de bandes et résistivité des semiconducteurs et isolants en fonction de la température

II ne peut exister d'isolant parfait qu'à 0 K. En effet à toute température finie, la probabilité de transition d'un électron de la bande de valence à la bande de conduction n'est pas nulle (fig. 2.28). Il en résulte une conduction due premièrement à la présence d'électrons dans la bande de conduction, secondement aux trous que le départ de ces électrons a créé dans la bande de valence.

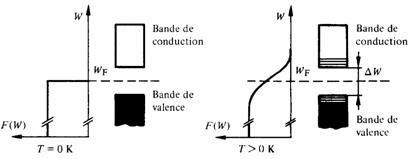
Fig. 2.28 Position de l'énergie de Fermi dans un isolant ou un semiconducteur

L'importance de cette conduction dépend très fortement de la largeur Wde la bande interdite. Seule la valeur de W distingue un semiconducteur d'un isolant. Un semiconducteur est un isolant à bande interdite étroite. Le tableau 2.29 résume le comportement électrique des matériaux selon leur valeur de W, à température ambiante.

Tableau2.29
Δ W	Comportement
> 5 eV	isolant
~ 1 eV	semiconducteur
< 0.15 eV	métallique

2.6.15 Critique du modèle unidimensionnel

II est évident que les cristaux réels sont à trois dimensions, et non une seule comme considéré jusqu'ici. L'objet de ce paragraphe est de montrer dans quelle mesure les résultats obtenus dans le cas unidimensionnel s'appliquent au cas réel.

Quelle que soit la direction dans laquelle il se déplace à l'intérieur d'un cristal, un électron est soumis à un potentiel périodique. Une solution du type unidimensionnel lui est donc applicable. La difficulté du problème tridimensionnel réside dans le fait que la position des bandes d'énergie varie avec l'orientation du déplacement par rapport aux axes cristallins.

Soit u₁ le vecteur unité désignant la direction dans le cristal, selon laquelle l'énergie supérieure de la bande de valence est minimum. Soit W_vl cette énergie, et W_c1 l'énergie inférieure de la bande de conduction pour la même direction. Soit a la période du potentiel selon u₁.

Soit u₂ le vecteur unité désignant la direction selon laquelle l'énergie supérieure de la bande de valence est maximum. Soit W_v2 cette énergie et W_c2 l'énergie inférieure de la bande de conduction pour la même direction. Soit b la période du potentiel selon u₂.

En reproduisant pour u₁ et u₂ la partie intéressante de la figure 2.24, on constate qu'il existe deux cas possibles (fg. 2.30).

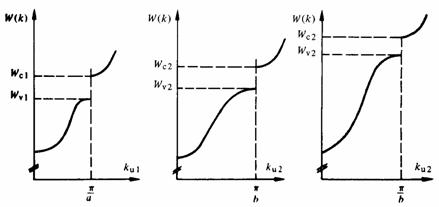
Fig. 2.30

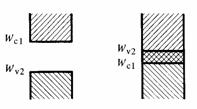
Fig. 2.31

Si W_vl  < W_v2  < W_c1 , il subsiste dans le cristal une bande interdite, de largeur W = W_c1 - W_v2. Ce cristal est donc semiconducteur ou isolant, selon la valeur de W (fg. 2.31).

Par contre, si W_v2 >W_c1, la bande interdite disparaît. La bande de conduction va donc se peupler avant que la bande de valence ne soit remplie. Il y a chevauchement des bandes de valence et de conduction, le cristal est conducteur (fig. 2.31).

La largeur de la bande interdite variant avec l'orientation, c'est la valeur minimum de W qui est mentionnée dans les tables, sauf indication contraire.

En résumé, les résultats du modèle unidimensionnel restent valables dans l'espace à trois dimensions, mais il apparaît dans cet espace une structure nouvelle caractérisée par le chevauchement de bandes permises.

2.6.16 Zones de Brillouin et surface de Fermi

La figure 2.24 montre que les limites des bandes d'énergies sont situées à la surface des zones de Brillouin (sect. 7.5) du cristal unidimensionnel. Il en est de même dans un cristal à trois dimensions.

Dans l'espace réciproque à trois dimensions, les fonctions W ( k_x, k_{y >}  k_z ) = C où C est une constante, sont des surfaces. Si C = W_F, la surface correspondante porte le nom de surface de Fermi.

L'analyse détaillée des propriétés électroniques d'un cristal passe donc par l'étude de la position de la surface de Fermi par rapport aux zones de Brillouin, en géométrie à trois dimensions.

2.6.17 Relation entre les bandes permises et les états de l'atome isolé

Imaginons un pseudo-cristal formé de N atomes identiques et dont la maille serait si grande que les atomes n'auraient pas d'interactions mutuelles. Les états électroniques de ce pseudo-cristal seraient ceux d'un atome multipliés N fois, ce qui ne serait pas contraire au principe de Pauli puisque les atomes sont isolés.

Diminuons par la pensée la maille de ce cristal, jusqu'à ce que les orbitales des électrons extérieurs se chevauchent. Alors, ces électrons forment un système, et leurs niveaux d'énergies possibles se répartissent en N niveaux voisins dont chacun peut accueillir deux électrons de spin opposés. L'intervalle d'énergie sur lequel se répartissent ces niveaux ne dépend pas de N, mais seulement du degré de recouvrement des orbitales, c'est-à-dire de l'intensité de l'interaction entre ces électrons. Plus l'interaction est intense, plus l'intervalle d'énergies est étendu.

En diminuant encore la maille, les orbitales des électrons appartenant à des couches plus profondes vont se chevaucher, provoquant une répartition semblable des niveaux correspondants. Ce mécanisme se répétera un certain nombre de fois jusqu'à ce que la maille corresponde à la distance interatomique normale du cristal (fig. 2.32).

On reconnaît, dans les intervalles d'énergie ainsi formés, les bandes dont l'existence a été démontrée au paragraphe 2.6.2.

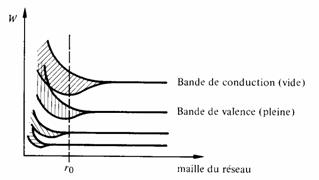
Fig. 2.32 Formation des bandes d'énergie dans un cristal (cas d'un isolant).

2.7 PROPRIÉTÉS DES SEMICONDUCTEURS

2.7.1 Semiconducteur intrinsèque

La structure de bandes représentée à la figure 2.28 est celle d'un semiconducteur pur, que l'on appelle en technique semiconducteur intrinsèque ou encore semiconducteur non dopé. La résistivité d'un tel semiconducteur est élevée, son usage est principalement de servir de matière première pour la fabrication de semiconducteurs extrinsèques ( 2.7.2 et 2.7.3).

Pour illustrer la situation au niveau atomique et par mesure de simplification, on ne représente que les liaisons des 4 électrons de valence du Si ou du Ge. On considère que les électrons de coeur  ( 10 pour le Si sur les couches 1 et 2; et 28 pour le Ge sur les couches 1, 2 et 3 ) ne participent pas aux phénomènes mesurables de conduction. Pour assurer la neutralité électrique du système, il est indispensable de considérer 4 protons pour compenser la charge des 4 électrons de valences. 

Le mécanisme de conduction dans un semiconducteur intrinsèque est schématisé à la figure 2.33.

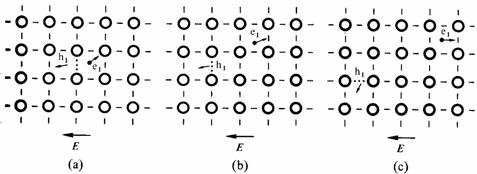
Fig. 2.33

Au stade (a), un lien de valence est rompu par l'énergie d'agitation thermique. Un électron e₁ est ainsi libéré, en d'autres termes il vient d'effectuer une transition de la bande de valence dans la bande de conduction, laissant un niveau vacant dans la bande de valence. La charge positive située dans la région de la valence brisée correspond à un trou, noté h₁. Cette région offre un niveau énergétique bas à tout électron se déplaçant dans le voisinage, de sorte que la probabilité que e₁ retourne occuper ce niveau est grande. En présence d'un champ appliqué, e₁ s'éloignera plus facilement de h₁, laissant à un électron venu de gauche sur la figure, le soin d'occuper le niveau vacant.

Les stades (b) et (c) de la figure 2.33 illustrent les déplacements successifs de e₁ et h₁ sous l'action du champ électrique.

On constate que, par nature, un semiconducteur intrinsèque possède le même nombre d'électrons que de trous.

2.7.2 Semiconducteur extrinsèque de type n

Un semiconducteur extrinsèque s'obtient par dopage, c'est-à-dire adjonction d'une très petite quantité d'atomes étrangers dans un semiconducteur intrinsèque.

Si les atomes étrangers ont un nombre d'électrons de valence supérieur à celui de l'hôte ( > 4 pour Si et Ge), on parle de semiconducteur extrinsèque type n, car les charges mobiles négatives (électrons) seront majoritaires. Les atomes de phosphore, d'arsenic ou d'antimoine possédant cinq électrons de valence sont couramment utilisés comme dopants dans les semiconducteurs de type n. Cest atomes doivent être compensés par 5 charges positives sur leur noyau pour conserver la neutralité électrique du système.

On appelle ces atomes donneurs car ils fournissent des électrons à la bande de conduction. Les donneurs se placent en position de substitution dans le réseau (fig. 2.34).

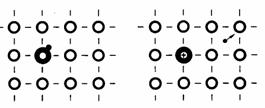
Fig. 2.34           o , atomes de l'hôte;            ⊕ , donneur;           • , électron libre.

Leur cinquième électron de valence, qui ne peut former de lien avec les atomes de l'hôte, reste à un niveau d'énergie plus élevé que les quatre autres. Du fait de la faible énergie le séparant de la bande de conduction, cet électron quittera donc facilement le donneur, faisant de ce dernier un ion positif.

Le dopage se traduit par l'apparition d'une bande très étroite d'énergies permises située à un niveau appelé niveau des donneurs, placé juste en-dessous de la bande de conduction (fig. 2.35). Cette nouvelle bande représente l'énergie des cinquièmes électrons liés. Elle se situe juste en-dessous de la bande de conduction, car le nombre de protons qui retiennent l'électron est plus grand que le nombre de protons de l'hôte. Un cinquième électrons au voisnage de l'hôte serait moins fortement attiré et trouverait sa place dans la bande de conduction.

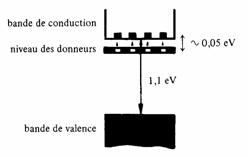
Fig. 2.35 Disposition des bandes dans un semiconducteur extrinsèque type n (silicium)

par attraction électrostatique aux atomes donneurs. Le faible intervalle d'énergie séparant le niveau des donneurs du bas de la bande de conduction, typiquement 0,01 à 0,1 eV, montre la fragilité de ces liaisons et le fait que les cinquièmes électrons sont quasi libres.

2.7.3 Semiconducteur extrinsèque de type p

Un autre type de semiconducteur extrinsèque s'obtient en dopant un semiconducteur intrinsèque au moyen d'atomes étrangers possédant un nombre d'électrons de valence inférieur à celui de l'hôte. Le bore, l'aluminium, le gallium et l'indium ont trois électrons de valence et sont utilisés couramment dans ce but.

Ces atomes étrangers portent ici le nom d'accepteurs car ils acceptent des électrons de la bande de valence, créant des niveaux vacants dans cette dernière. Les trous deviennent ainsi les porteurs de charges mobiles majoritaires et l'on appelle le semiconducteur résultant de ce dopage, un semiconducteur de type p.

Les accepteurs occupent également une position de substitution mais il manque cette fois un électron de valence pour lier complètement l'atome étranger à ses voisins (fig. 2.36). En d'autres termes, un état électronique de basse énergie reste inoccupé au voisinage de l'atome étranger. La probabilité est grande que cet état soit ultérieurement occupé par un électron provenant d'un lien de valence voisin, et déplacé sous l'effet de l'énergie d'agitation thermique, et éventuellement d'un champ appliqué. Ce transfert correspond au déplacement d'un trou.

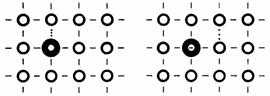
Fig. 2.36 o, atomes de l'hôte;            ⊕, accepteur;              ¦, position du trou.

L'état électronique laissé vacant par l'atome étranger correspond à une bande d'énergie très étroite, située à un niveau d'énergie appelé niveau des accepteurs placé juste au-dessus du sommet de la bande de valence (fig. 2.37). Pour justifier cette position il suffit de se rappeler que l'atome accepteur possède 1 proton de moins que l'hôte. L'attraction de l'électron du "quatrième" électron est donc moins forte au voisinage de l'accepteur. Le faible intervalle d'énergie séparant la bande des accepteurs du haut de la bande de valence, typiquement 0,01 à 0,1 eV, explique le transfert important d'électrons de la bande de valence vers celle des accepteurs dès qu'il y a un peu d'agitation thermique.

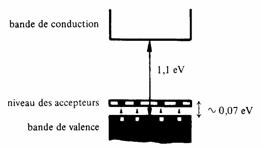
Fig. 2.37 Disposition des bandes dans un semiconducteur extrinsèque type n (silicium)

2.7.4 Nombre volumique d'électrons dans un semiconducteur intrinsèque

Seule la portion inférieure de la bande de conduction peut contenir en réalité des électrons, en raison de la convergence rapide de la distribution de Fermi-Dirac aux énergies supérieures.

Dans cette portion, la fonction W(k) (fig. 2.24) est assimilable à une parabole, d'autre part la masse effective m ∗ de l'électron est pratiquement constante (tab. 2.26). On retrouve, localement, les conditions dans lesquelles la densité des états a été calculée pour le cas de l'électron libre. L'équation (2.61) prend ici la forme :

       (2.143)

avec

                 (2.144)

où W_c désigne l'énergie inférieure de la bande de conduction. Le nombre volumique n d'électrons présents dans la bande de conduction s'exprime par

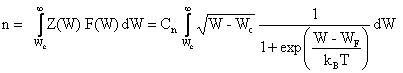       (2.145)

La limite supérieure d'intégration devrait correspondre à l'énergie maximum de la bande de conduction. La convergence rapide de F(W) permet de fixer cette limite à l'infini. Il en résulte une première simplification dans le calcul de (2.145). Une seconde simplification provient du fait que 1 peut être négligé face à l'exponentielle, au dénominateur de F(W). En effet, dans un semiconducteur intrinsèque, l'énergie de Fermi est très proche du centre de la bande interdite ( 2.7.6). Pour une largeur de celle-ci de 0,7 eV seulement, on obtient déjà à 20°C :

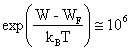              (2.146)

L'équation (2.145) devient donc :

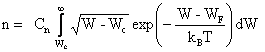               (2.147)

En effectuant le changement de variable :

                         (2.148)

Il vient

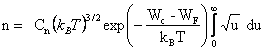           (2.149)

d'où par (7.8.3)

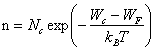               (2.150)

avec

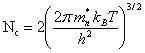                          (2.151)

L'exponentielle dans (2.150) représente une très bonne approximation de la probabilité d'occupation d'un état à l'énergie W_c. On peut donc interpréter l'équation (2.150) de la manière suivante : la bande de conduction fournit un nombre volumique d'électrons égal à celui que fournirait un niveau unique, situé à W_c, et possédant N_c états possibles par unité de volume. A 20°C et pour m∗_n = m_n, on a :

N_c = 2,42 10²⁵ m^-3                (2.152)

Le silicium possède 5 10²⁸ atomes par m³. Pour ce matériau dont la largeur de la bande interdite vaut 1,12 eV, l'expression (2.150) donne, à 20°C, n = 5,7 10¹⁵ m^-33. A cette température, le silicium pur ne possède donc qu'un électron libre pour 9 10¹² atomes.

2.7.5 Nombre volumique de trous dans un semiconducteur intrinsèque

Le calcul du nombre volumique de trous est en tous points semblables au développement du paragraphe précédent. Le haut de la bande de valence seul peut présenter des états vacants. Dans cette région, la fonction W k), tracée à la figure 2.24, possède encore une allure parabolique. Par analogie avec (2.143), on peut donc écrire:

 

             (2.153)

où

                 (2.154)

W_v désigne l'énergie maximum de la bande de valence et m^∗_p la masse effective du trou, pratiquement constante dans l'intervalle d'énergies considéré (tab. 2.26).

Le nombre volumique p de trous dans la bande de valence est donné par l'expression:

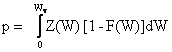          (2.155)

Dans F(W), le terme exp [(W - W_F) /k_B T] est suffisamment petit pour poser :

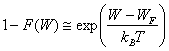         (2.156)

de sorte que (2.155) prend la forme :

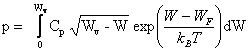             (2.157)

Cette équation s'intègre par le changement de variable

     (2.158)

Qui permet l'usage de (7.8.3), et conduit à

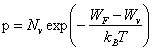           (2.159)

avec

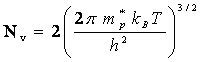              (2.160)

2.7.6 Energie de Fermi dans un semiconducteur intrinsèque

Dans un semiconducteur intrinsèque, le nombre volumique d'électrons dans la bande de conduction est égal au nombre volumique de trous dans la bande de valence. Cette égalité s'écrit, grâce aux équations (2.150) et (2.159),

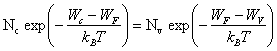             (2.161)

Les énergies W_c et W_v, étant connues, cette expression permet de trouver W_F. En prenant le ln des deux membres de (2.151) il vient

            (2.162)

d'où, en tenant compte de (2.151) et (2.160)

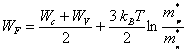             (2.163)

Même pour une différence relativement importante entre m^∗_p et m^∗_n, le terme en ln dans (2.163) reste peu important devant (W_c + W_v) /2. On en déduit que dans un semiconducteur intrinsèque, l'énergie de Fermi est très proche du milieu de la bande interdite.

2.7.7 Remarque

Il est intéressant de constater qu'il n'est pas nécessaire de connaître W_F pour calculer n ou p dans un semiconducteur intrinsèque. Posons, pour un tel semiconducteur

n_i = n = p               (2.164)

Par (2.150) et (2.159) il vient

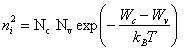         (2.165)

L'énergie de Fermi a disparu de cette expression. La largeur de la bande interdite y joue par contre un rôle important, comme on devait s'y attendre.

2.7.8 Règle du produit pn

Unsemiconducteur extrinsèque se distingue d'un semiconducteur intrinsèque par la position de l'énergie de Fermi dans la bande interdite, ainsi qu'on va le voir au paragraphe suivant. La relation (2.165), indépendante de WF est aussi valable pour un semiconducteur extrinsèque. Dans un tel semiconducteur, n est différent de p

( 2.7.11) mais, ainsi que le montre (2.165) le produit pn est une constante indépendante du dopage, à température donnée:

p n = n_i²                  >(2.166)

Ce résultat constitue la règle du produit pn. Il est d'une grande utilité dans l'étude des semiconducteurs extrinsèques.

2.7.9 Energie de Fermi dans un semiconducteur extrinsèque

Considérons le cas le plus général d'un semiconducteur recevant des donneurs et des accepteurs. Avant dopage, le semiconducteur est électriquement neutre. Les atomes des dopants ajoutés sont neutres également, de sorte que le semiconducteur dopé doit être neutre lui aussi.

Cette constatation permet de déterminer le niveau de Fermi dans un semiconducteur dopé. Soient

  N_d le nombre volumique des donneurs et W_d l'énergie à laquelle est situé le niveau des donneurs,

   N_a et W_a les valeurs correspondantes concernant les accepteurs.

On trouve des charges négatives :

   dans la bande de conduction (électrons). Leur nombre volumique est donné par (2.150)

   dans la bande des accepteurs (ions), leur nombre volumique vaut

N_a^- = N_a F (W_a)                        (2.167)

On trouve des charges positives :

   dans la bande de valence (trous). Leur nombre volumique est donné par (2.159)

   dans la bande des donneurs (ions), leur nombre volumique vaut

N_d⁺ = N_d [1 -F(W_d)]                (2.168)

Les expressions (2.167) et (2.168) peuvent être évaluées en recourant aux mêmes approximations concernant la distribution de Fermi-Dirac que celles admises pour le calcul de n et p.

 

           

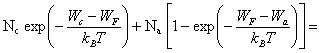
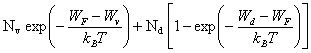        (2.169)

La résolution numérique de (2.169) ne pose pas de problèmes particuliers, toutefois il est utile de disposer d'une solution analytique approchée. Celle-ci sera obtenue au prix de deux approximations.

On considère premièrement que (W_F-W_a) et (W_d-W_F) sont suffisamment grands par rapport à k_BT pour que l'équation (2.169) puisse être ramenée à la forme suivante :

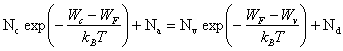    (2.170)

On vérifiera sur la figure 2.38 que cette simplification est admissible dans un large domaine de température. Sous une forme plus condensée, (2.170) s'écrit encore :

n +N_a = p+N_d               

 

Deuxièmement, on se limite au seul cas intéressant en pratique, celui où N_d différent de N_a. Il suffit d'un faible écart entre N_d et N_a pour que n et p diffèrent l'un de l'autre de plusieurs ordres de grandeurs ( 2.9.6). Si N_d > N_a, le nombre volumique des trous est négligeable devant le nombre volumique des électrons. Alors, la solution de (2.170) s'obtient très simplement en prenant le logarithme des deux membres de cette équation. Il vient :

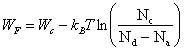        (2.172)

Si N_a > N_d, c'est le nombre volumique des électrons qui est négligeable par rapport à celui des trous. Dans ce cas, (2.170) conduit à la solution N

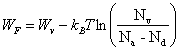                 (2.173)

 

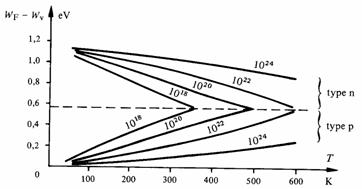
Fig. 2.38 Energie de Fermi dans le silicium extrinsèque en fonction de la température. En paramètre, le nombre volumique de donneurs, respectivement d'accepteurs. D'après [111].

On constate, sur la figure 2.38, que dans un large domaine de températures, W_F varie linéairement avec la température, en accord avec (2.172) et (2.173). Toutefois la pente dW_F / dT donnée par ces équations est inférieure à celle de la figure.

La fonction de Fermi-Dirac apparaissant dans les équations (2.167) et (2.168) aurait dû être modifiée par rapport à (7.43) en raison de la dégénérescence des niveaux des donneurs et des accepteurs [12]. Les simplifications introduites dans la résolution de (2.169) ont rendu cela inutile.

2.7.10 Comportement des semiconducteurs extrinsèques aux températures extrêmes

La variation de W_F reportée à la figure 2.38 explique le comportement des semiconducteurs extrinsèques aux températures extrêmes.

Aux basses températures l'énergie de Fermi dans un semiconducteur de type n se place entre le bas de la bande de conduction et le niveau des donneurs. Le semiconducteur se comporte donc comme un semiconducteur intrinsèque, dont le niveau des donneurs joue le rôle de bande de valence. Dans un semiconducteur de type p, W_F se place entre le haut de la bande de valence et le niveau des accepteurs. Le semiconducteur se comporte donc aussi comme un semiconducteur intrinsèque, dont le niveau des accepteurs joue le rôle de bande de conduction.

Aux températures élevées l'énergie de Fermi rejoint le milieu de la bande interdite, aussi bien dans les semiconducteurs de type n que de type p. Ces semiconducteurs se comportent alors comme des semiconducteurs intrinsèques. Dans la bande de conduction (type n) le nombre d'électrons en provenance de la bande de valence surpasse nettement le nombre d'électrons en provenance des donneurs. Réciproquement, dans la bande de valence (type p), le nombre de trous correspondant au départ d'électrons vers la bande de conduction surpasse nettement le nombre de trous formés grâce aux accepteurs.

2.7.11 Occupation des bandes d'un semiconducteur, cas général

L'occupation des bandes d'un semiconducteur, déterminée par la densité des états, la distribution de Fermi-Dirac et la valeur de W_F est représentée schématiquement à la figure 2.39. On remarquera en particulier l'apparition massive d'électrons dans la bande de conduction des semiconducteurs de type n, et de trous dans la bande de valence des semiconducteurs de type p.

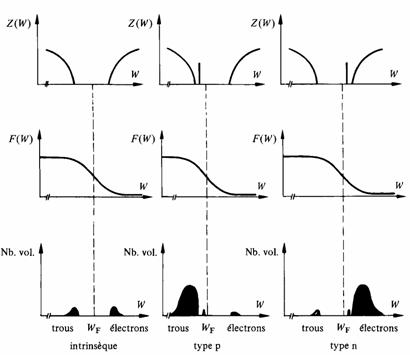
Fig. 2.39

Les nombres volumiques d'électrons et de trous dans les semiconducteurs extrinsèques se calculent aisément. Soient n_n, p_n et n_p, p_p ces grandeurs dans les semiconducteur de type n et p respectivement.

On considère tout d'abord le cas des semiconducteurs de type n. Les équations (2.166) et (2.171) constituent un système à deux inconnues n, c'est-à-dire n_n et p, c'est-à-dire p_n. En tirant n_n de ce système on obtient :

             (2.174)

On sait ( 2.9.6) que << n. D'autre part, N_d est très grand devant N_a .Par conséquent :

              (2.175)

On montre de la même manière

               (2.176)

 

En résumé:

• •dans un semiconducteur de type n, le nombre volumique des électrons est approximativement égal au nombre volumique des donneurs;
• •dans un semiconducteur de type p, le nombre volumique de trous est approximativement égal au nombre volumique des accepteurs.

2.7.12 Conductivité d'un semiconducteur

La conductivité d'un semiconducteur s'obtient en sommant les contributions au courant provenant des électrons d'une part, des trous d'autre part. Pour chaque porteur de charge pris séparément, les développements du paragraphe 2.3.1 restent valables, de sorte que l'équation (2.20) est immédiatement généralisable sous la forme suivante :

s = n e µ_n + p e µ_p          (2.177)

 

La mobilité µ_p des trous est définie de la même manière que la mobilité µ_n des électrons (2.14). Chacune de ces mobilités possède deux composantes. L'une, µ_n,ph respectivement µ_p,ph, dépend de l'interaction des porteurs de charge avec les phonons. L'autre, µ_n,im, µ_p,im, dépend de l'interaction des porteurs de charge avec les autres types de défauts cristallins, qui sont ici principalement les ions des Les équations (2.14) et (2.26) donnent la règle d'additivité de ces grandeurs :

           (2.178)

 

L'indice s représente l'indice n, respectivement l'indice p. Le calcul de µ_s,im et µ_{s, im} est une tâche compliquée. En fonction de la température, ces grandeurs suivent approximativement les lois suivantes :

              (2.179)

            (2.180)

 

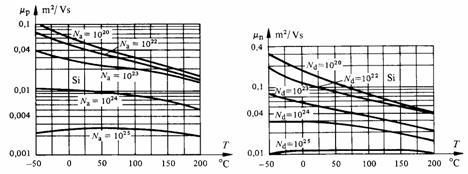
Fig. 2.40 Mobilité des électrons et des trous dans le silicium, en fonction de la température et du nombre volumique des dopants en m^-3. D'après [13].

Dans (2.180), N_im représente le nombre volumique des atomes étrangers. Les expressions (2.179) et (2.180) sont en accord avec les considérations émises au paragraphe 2.2.2 à propos des métaux, à savoir que l'interaction des porteurs de charges avec les impuretés est prépondérante à basse température, alors que l'interaction avec les phonons l'emporte quand la température croît (fig. 2.40).

A température ordinaire, le logarithme de la résistivité varie assez linéairement en fonction du logarithme du nombre volumique des atomes étrangers ainsi qu'en témoigne la figure 2.41.

2.7.13 Matériaux semiconducteurs

La structure des bandes et en particulier la largeur de la bande interdite dépendent autant de la structure cristalline que de la nature des atomes. L'influence de la

 

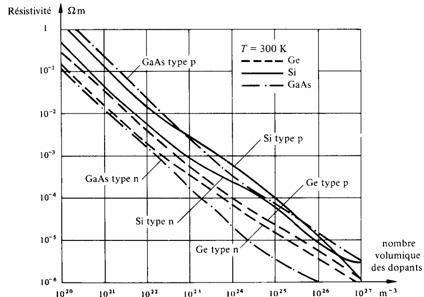
Fig. 2.41 Résistivité du silicium, du germanium et de l'arséniure de gallium, à 300 K, en fonction du nombre volumique des dopants. D'après [13].

structure cristalline est illustrée par l'exemple classique du carbone qui, sous forme de diamant est un isolant, et sous forme de graphite un conducteur.

Les matériaux semiconducteurs se recrutent essentiellement dans les classes suivantes :

• • éléments du groupe IV B de la table de Mendéléev. Ils possèdent la structure du diamant (fig. 1.22),

• • composés formés d'éléments des groupes IIIB et VB, ou des groupes IIB et VI B. Ces composés présentent la structure de la blende (fig. 2.44) ou celle du sulfure de zinc hexagonal, toutes deux proches de la structure du diamant.

A la première classe appartiennent le germanium et le silicium dont l'importance économique est bien connue. Dans ces matériaux les liaisons sont covalentes. L'énergie de liaison est plus faible dans le germanium que dans le silicium, c'est pourquoi la largeur W de la bande interdite est plus faible dans le germanium que dans le silicium (tab. 2.42).

Tableau 2.42
Elément	Ge	Si	C (Diamant)
Δ W [eV]  (à 20°C)	0,66	1,12	5,3

Le dopage du germanium et du silicium s'effectue au moyen d'éléments du groupe IIIB pour les types p et du groupe VB pour les types n. Les composants électroniques utilisant le silicium dopé peuvent fonctionner à des températures plus élevées (~ 200°C) que ceux utilisant le germanium (~ 100°C). En effet, la bande interdite plus large du silicium augmente la température à laquelle ce matériau, à l'état dopé, retrouve un comportement de semiconducteur intrinsèque le rendant impropre à assurer le fonctionnement d'une jonction (vol. VII).

Le recours aux composés formés d'éléments des groupes III B et V B augmente le choix des Δ W et des mobilités disponibles, comme en témoigne le tableau 2.43. Tous les composés du tableau 2.43 possèdent la structure de la blende, dérivée de la structure du diamant par le remplacement des atomes de carbone par les atomes des

Tableau 2.43
Matériau	Δ W [eV]	µn [m2/Vsec]	µp [m2/Vsec]
Ga	2,25	0,045	0,002
AISb	1,60	0,040	0,020
GaAs	1,42	0,85	0,045
InP	1,27	0,60	0,016
GaSb	0,70	0,50	0,085
InAs	0,33	2,3	0,010
InSb	0,18	8,0	0,070

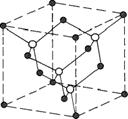
Fig. 2.44 Structure de la blende.

 

groupes III B et V B, de façon telle que chaque atome d'un groupe soit au centre d'un tétraèdre dont les sommets sont formés d'atomes de l'autre groupe (fig. 2.44).

Dans la structure de la blende, les liens de valence ont encore un caractère covalent dominant, avec toutefois une légère composante ionique (5 à 10% de l'énergie de liaison). Cette composante serait responsable de l'augmentation de AW dans un composé, par rapport à la valeur de AW dans le semiconducteur correspondant du groupe IV B. Dans GaAs par exemple, A W = 1,42 eV, alors que dans le germanium, élément situé entre le gallium et l'arsenic sur la table de Mendéléev, W = 0,66 eV.

L'élaboration des composés semiconducteurs est plus délicate que celle des semiconducteurs du groupe IVB car, au problème de la pureté chimique s'ajoute celui des concentrations atomiques relatives des deux constituants. La différence entre ces concentrations ne doit pas excéder une valeur approximativement égale au nombre volumique tolérable des impuretés. En effet, si la concentration en atomes du groupe III B est légèrement inférieure à celle du groupe VB, des lacunes apparaîtront aux sites normalement occupés par les atomes du groupe IIIB. Ces lacunes se comporteront comme des accepteurs. Réciproquement la présence de lacunes aux sites normalement occupés par des atomes du groupe V B équivaut à un dopage par des donneurs.

L'arséniure de gallium GaAs est l'un des composés semiconducteurs les plus intéressants. Il est très largement utilisé dans les composants optoélectroniques (chap. VII.9). Ses avantages résident dans une valeur de W relativement élevée, associée à des niveaux de donneurs et d'accepteurs très proches des bandes de valence et de conduction. Il en résulte des températures de fonctionnement possibles élevées d'une part, une grande efficacité des dopants à température ambiante d'autre part. L'arséniure de gallium peut être dopé par le germanium, qu'un traitement thermique adéquat permet de placer en substitution, soit dans un site  normalement occupé par un atome IIIB (GaAs type n) soit dans un site normalement occupé par un atome VB (GaAs type p).

Dans les composés formés d'éléments appartenant aux groupes II B et VI B, la part de l'énergie de liaison correspondant à la valence ionique s'accroît encore par rapport à celle de la covalence, avec l'augmentation de W dont il vient d'être question. Les composés CdS, CdSe et CdTe sont des représentants de cette catégorie de semiconducteurs, fréquemment utilisés comme détecteurs de rayonnement lumineux, et infrarouge pour Cd Te.

Notons pour terminer, qu'un grand nombre d'autres substances ont un comportement de semiconducteur, sans que cette propriété présente toujours l'importance technologique des exemples cités ci-dessus.

 

2.7.14 Elaboration des matériaux semiconducteurs

Les matériaux semiconducteurs entrant dans la fabrication de composants électroniques doivent posséder deux qualités

    la pureté chimique, sans laquelle les effets du dopage réalisé à de très faibles concentrations, ne peuvent se manifester;

        la perfection cristalline la meilleure possible, car les défauts de structures provoquent localement l'apparition de niveaux d'énergie supplémentaires. Qu'une jonction pn (vol. VII) contienne un joint de grain par exemple, et l'effet redresseur peut disparaître complètement, ou tout au moins diminuer d'efficacité. Un nombre élevé de dislocations est susceptible d'avoir le même effet.

La pureté chimique est obtenue par pyrolyse ou par la méthode de la fusion de zone. Dans cette dernière méthode (fig. 2.45), l'échantillon de forme cylindrique est placé dans un creuset de graphite. Un enroulement se déplaçant lentement induit des courants de Foucault faisant localement fondre le semiconducteur. Dans son mouvement, la zone liquide entraîne les impuretés de l'échantillon, laissant le matériau qui se solidifie derrière elle dans un état de pureté plus grande.

 

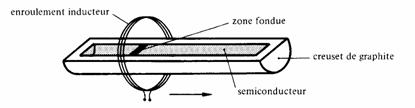
Fig. 2.45 Principe de la méthode de la fusion de zone.

 

L'opération se passe sous atmosphère contrôlée, pour éviter toute pollution externe du semiconducteur. Elle doit être répétée un certain nombre de fois pour qu'une pureté suffisante soit atteinte. Industriellement, on évite ces répétitions en plaçant plusieurs enroulements inducteurs les uns derrière les autres.

Le processus de purification sera décrit dans le cas d'un semiconducteur ne présentant qu'un seul type d'impureté, abaissant par exemple le point de fusion. Le degré de pureté initial étant supposé relativement élevé, il suffit de considérer une petite fraction du diagramme de phase (chap. 5) correspondant aux faibles concentrations

 

Fig. 2.46

 

de l'atome étranger. Dans cette région, le liquidus et le solidus peuvent être approchés par deux droites concourantes (fig. 2.46).

Soit C_o la concentration initiale de l'impureté. Dans la zone liquide initiale, encore immobile, la concentration d'impuretés est aussi C_o.

Un déplacement de l'inducteur d'une valeur dx vers la droite provoque la solidification à gauche d'une zone d'épaisseur dx dans laquelle la concentration en impuretés est abaissée à C_s0, tandis qu'une nouvelle zone fond vers la droite.

 

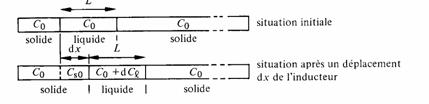
Fig. 2.47

Soit C_s la concentration en impuretés de la phase solide en contact avec la phase liquide, et C_l la concentration en impuretés de la phase liquide, C_l étant supposé homogène dans la zone fondue (fig. 2.47). C_l et C_s sont des fonctions de x, et l'on a d'après la figure 2.46

 

C_s (x) = K C2 (x)

où K est une constante appelée facteur de ségrégation. Lors d'un déplacement dx de la zone fondue, le bilan des impuretés dans cette zone de longueur L s'écrit

L dC_l = C_O dx - C_s (x) dx            (2.182)

 soit encore en exprimant C_l au moyen de C_s qui est la variable intéressante

 dC_s = K/L(C_o -C_s)dx              (2.183)

d'où

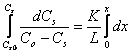            (2.184)

Et par integration:

          (2.185)

Cette expression permet d'évaluer la distance x sur laquelle le procédé est d'un rendement intéressant.

La pureté chimique requise étant atteinte, il reste à assurer une perfection cristalline suffisante, c'est-à-dire à mettre l'échantillon sous la forme d'un monocristal. La méthode de Czochralski (fig. 2.48) est généralement utilisée pour cette opération.

Le semiconducteur est porté, dans un creuset, à une température très légèrement supérieure au point de fusion. Un germe, c'est-à-dire un petit monocristal du même

 

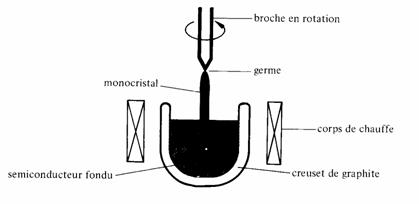
Fig. 2.48 Tirage d'un monocristal par la méthode de Czochralski.

semiconducteur, orienté correctement et fixé à l'extrémité d'une broche est mis en contact avec la surface du liquide. Dans un premier temps, on laisse le germe fondre très légèrement afin qu'il soit parfaitement mouillé par le semiconducteur liquide. Ensuite on extrait par la broche, la quantité de chaleur juste nécessaire pour que le liquide en contact avec le germe se solidifie progressivement, en prolongeant les axes cristallins du germe. Au cours de cette phase, la broche est mise en rotation et lentement retirée vers le haut, de façon à maintenir l'interface liquide-solide proche de la surface. La rotation prévient l'apparition de différences de température qui nuiraient à la régularité de forme du monocristal. Le plus souvent, ce sont des échantillons de 10 cm de diamètre et de 1 m de longueur qui sont ainsi produits, pour être ensuite découpés en minces plaquettes sur lesquelles seront fabriqués les composants: diodes, transistors, circuits intégrés, etc. (chap. VII.10).