
|
|
back
MENU
|
|
Private
|

Model
Supercapacitor electrical equivalent model
The double-layer capacitor is a physical component which hasn't only a requested capacitance, but also an unavoidable parasitic inductance due to its geometry, a series resistance due to the electronic and ionic conductor ohmic resistances and a parallel resistance due to the leakage current between the electrodes.
The equivalent series resistance ESR, which is a combination of the series resistance Rs and the parallel resistance Rp (see fig. 1), is responsible for the electrical losses which generate the internal heating.
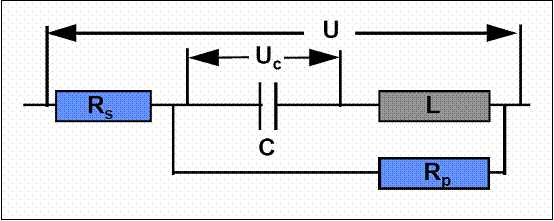
Figure 1: Basic ultracapacitor electrical equivalent circuit.
To get high
power, it is absolutely necessary to have a low ESR. The parallel resistance Rp
has an effect visible only at very low frequency (below the milihertz
range). It is responsible for the capacitor self discharge time. Its value must
be as high as possible to limit the leakage current. The time constant t of the self
discharge is equal to t = Rp C.
The transmission-line basic model used to
describe the frequency behavior of the capacitance and the series resistance
has been originally proposed by de Levie [i]. This theory doesn't take into account the voltage and temperature
dependences of the capacitance and series resistance. A simple model which
considers an additional linear dependence of the capacitance on the tension has
been proposed by Zubieta et al. [ii]. Similar models have been used also by Dougal
et al. [iii] and Belhachemi et al. [iv]. The capacitance is composed by a constant part Co
and a linear voltage dependent one ![]() where Kv is a coefficient which depends on
the technology. The total capacitance at the voltage U is given by:
where Kv is a coefficient which depends on
the technology. The total capacitance at the voltage U is given by:
![]() (1)
(1)
The relation between the current and the voltage must be derived from the relation between the current and the charge which remains always true.
![]() (2)
(2)
Substituting the Q expression as a function of U and C, taking into account the indirect dependence of C with the time, it is easy to show that the current is given by equation:
![]() [v](3)
[v](3)
By analogy with the classical relation, one may define a differential supercapacitor capacitance as:
![]() (4)
(4)
The stored energy is equal to the time integral of the power that leads to the relation :
![]() (5)
(5)
In conclusion, the current and the energy for a given voltage are bigger than what they were expected on the base of the classical expressions in the case of constant capacitance.
The capacitance and the series resistance have values which are not constant over the frequency spectrum. The performances may be determined with an Impedance Spectrum analyzer [vi]. To take into account the voltage, the temperature and the frequency dependencies, a simple equivalent electrical circuit has been developed by Rafik et al (Fig. 2). It's a combination of the De Levie frequency model and Zubieta voltage model with the addition of a function to take into account the temperature dependence.
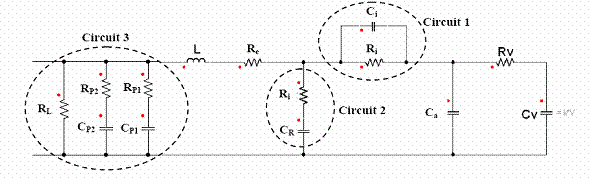
Figure 2: Equivalent circuit for capacitance and series resistance dependences as a function of frequency, voltage and temperature.
The equivalent scheme is composed of a fixed capacitance Co connected in parallel with a variable capacitance Cv. Cv increases linearly with the voltage. The series resistance and capacitance voltage dependencies are active only in the low frequency domain which may be taken into account with the simple RvCv circuit. To get the frequency dependence, the resistance RT and the capacitance CR have been introduced in circuit 2. Their behaviour is the one of a low pass filter with a cut off frequency τ = RTCR. "Circuit 1" has been added to take into the thermal dependence. Circuit 3 shown is required to complete the modelling regarding the leakage current and the charge redistribution. It includes two RC parallel branches with two different time constants. It also includes a parallel RF resistance which gives the long time leakage current.
Basically the available capacitance is maximal at low frequency. This may be explained with the longer time available for the ions in the electrolyte to reach the surface which is located deep in the carbon pores. At higher frequency, only the superficial carbon surface is accessible for the ions. The capacitance is consequently much smaller.
The series resistance is composed of an electronic and an ionic part. The electronic contribution comes from the ohmic resistance in the conductor and in the carbon particles. The ionic contribution comes from the ions mobility in the electrolyte.
[i] de Levie R. Advances in Electrochemistry and Electrochemical Engineering 1967;6:329-97.
[ii] Zubieta L, Bonert R, Dawson F. Considerations in the design of energy storage systems using double-layer capacitors. IPEC Tokyo 2000; 1551.
[iii] Dougal RA, Gao L, Liu S. Ultracapacitor model with automatic order selection and capacity for dynamic system simulation. J Power Sources 2004;126:250-7.
[iv] Belhachemi F, Raël S, Davat B. A physical based model of power electric double-layer supercapacitors", IEEE-IAS'00, 2000, Roma.
[v] Hermann V, Schneuwly A, Gallay R. High power double-layer capacitor developments and applications, ISE2001, San Francisco.
[vi] Kurzweil P, Fischle HJ. A new monitoring method for electrochemical aggregates by impedance spectroscopy. J Power Sources 2004;127:331-40.
Source: Garmanage: Roland Gallay