|
|
back |
Annexes
7.2 Distribution statistique de Maxwell
7.2.1 Champ d'application
La distribution de Maxwell régit le comportement d'un ensemble de particules ponctuelles de nature classique,
en équilibre thermodynamique,
n'interagissant pas entre elles sauf à l'occasion de collisions qui sont des chocs élastiques,
non soumises à l'action d'un potentiel extérieur.
Un tel ensemble de particules est appelé gaz parfait. Les atomes d'un gaz parfait sont souvent considérés comme des particules sans interactions mutuelles. Il faut entendre par là qu'elles ne créent aucun potentiel, origine de forces d'interaction d'une certaine portée, comme les forces de valence par exemple. Mais ces particules ont bien une certaine forme d'interaction lors des chocs ! L'établissement d'un équilibre thermodynamique serait impossible autrement.
7.2.2 Démonstration
De façon précise, la distribution de Maxwell répond à la question suivante. Quel est le nombre dN de particules possédant, à un instant donne, une vitesse dont les composantes sont comprises entre vx, vx + dvx; vy, vy + dvy; vz, vz + dvz. La réponse est de la forme :
dN = N f(vx,vy,vz) dvx dvy dvz
La probabilité qu'une particule ait une certaine composante de vitesse selon un axe est totalement indépendante des composantes qu'elle possède selon les deux autres axes. La validité de ce postulat de Maxwell peut être vérifiée par la distribution de Bolzmann (sect. 7.3), établie par d'autres voies, et dont la distribution de Maxwell est un cas particulier.
On posera donc :
f(vx,vy,vz) = g(vx) g(vy) g(vz) (7.4)
Les fonctions g représentent les distributions des vitesses selon chaque axe. Soit
(7.5)
la vitesse scalaire d'une particule. La probabilité pour une particule que cette vitesse soit comprise dans un intervalle v, v + dv quelconque doit être indépendante de la direction, faute de quoi l'on aurait à faire à un gaz s'écoulant spontanément dans certaines directions, ce qui est contraire a la condition d'équilibre posée. Par conséquent,
f(vx,vy,vz) = f(v) = g(vx) g(vy) g(vz) (7.6)
Cette équation, apparemment très générale, suffit pour établir la distribution de Maxwell, le recours à des arguments supplémentaires n'étant nécessaire que pour déterminer la valeur de deux paramètres.
Les fonctions f et g satisfaisant (7.6) sont obtenues par la procédure suivante : on prend le logarithme naturel des deux membres de (7.6),
ln f(vx,vy,vz) = ln f(v) = ln g(vx) + ln g(vy)+ ln g(vz) (7.7)
puis la dérivée partielle par rapport à vx de (7.7),
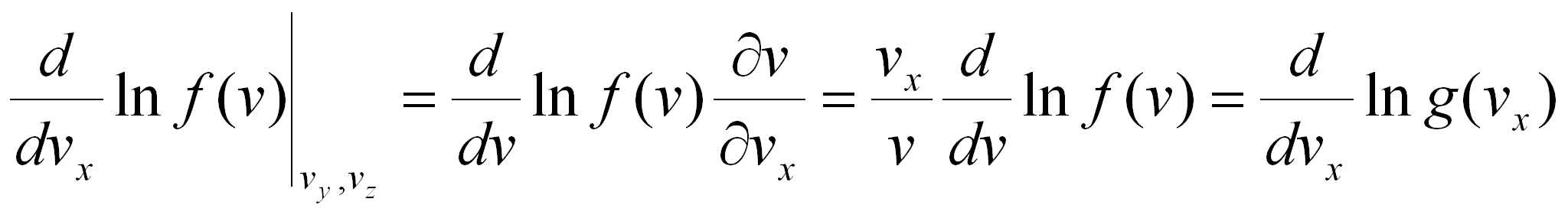(7.8)
Cette équation est à variables séparées. On peut l'écrire sous la forme :
(7.9)
En dérivant successivement les membres de (7.7)
par rapport a vy et vz,
on obtient de
Chaque terme de (7.10) dépend d'une variable
différente, tous ces termes sont donc égaux
a une seule et même constante que l'on appellera –13. En
intégrant (7.9) on obtient ainsi :
La constante d'intégration Cest
détermine par la condition de normalisation :
Cette intégrale se calcule par (7.8.1). Il vient:
Il reste
à déterminer la constante (3. La théorie des gaz parfaits montre que l'énergie
des particules, qui est réduite à leur énergie cinétique de translation, est proportionnelle
à la température absolue et vaut ½ kBT, par
degré de liberté. Par conséquent,
En portant (7.11) et (7.13) dans (7.14), et en effectuant l'intégration on obtient :
b = m / 2kBT (7.15)
Les expressions de g(vy) et g(vz) sont semblables à (7.16). La distribution f (vx,,vy,vz)
est donc connue par (7.6) :
Dans l'espace des vitesses, tous les points représentatifs des particules ayant une même vitesse scalaire v sont situés
sur une sphère de rayon v. Le nombre de particules possédant
des vitesses scalaires comprises entre v et v + dv est proportionnel
au volume 4 PI v2 dv situe entre les sphères de rayon v et v + dv. Cette
propriété de l'espace des vitesses
permet d'expliciter (7.3) en termes de v uniquement. Il vient :
C'est la distribution de Maxwell.
La signification de dN diffèrelégèrement dans (7.3) et dans (7.18) ou dN représente le nombre de particules dont la vitesse scalaire est comprise entre v
et v + dv. On vérifie aisément que (7.18)
satisfait la relation de normalisation
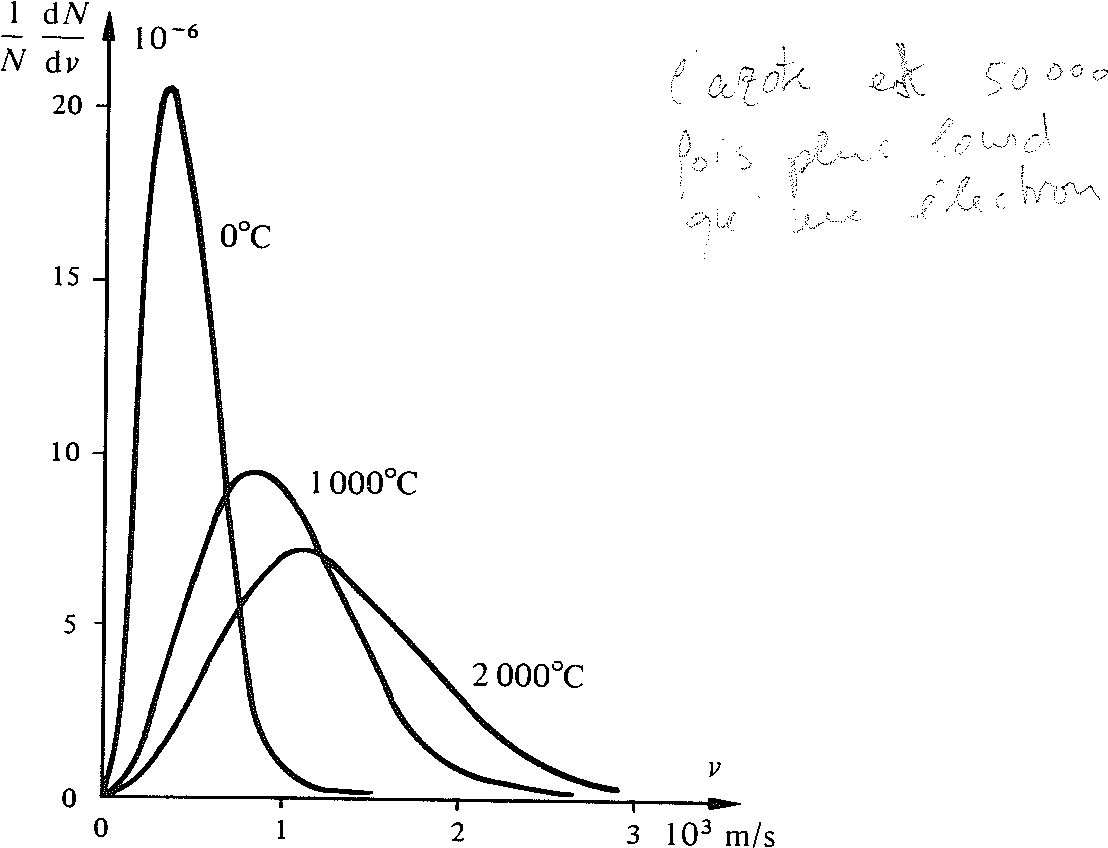
7.2.3 Représentation graphique
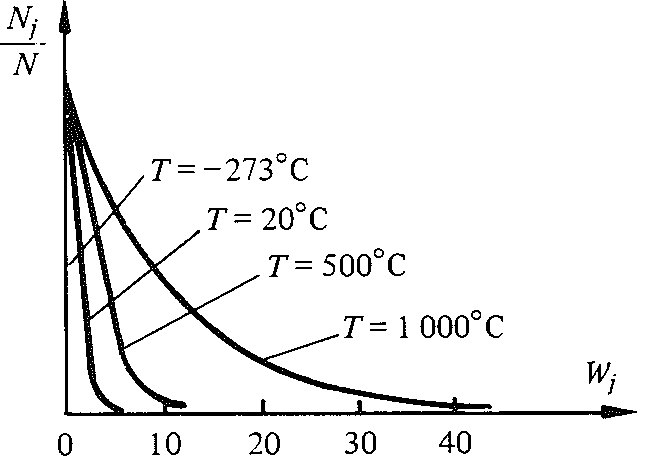
La figure 7.1 représente la distribution de Maxwell pour l'azote, à différentes températures.
Fig. 7.1
7.3.1 Champ d'application
La distribution de Boltzmann
régit le comportement d'un ensemble de particules ponctuelles
de nature classique,
en équilibre thermodynamique,
sans interactions mutuelles au sens du paragraphe 7.2.1,
susceptibles d'être soumises à l'action d'un potentiel extérieur.
Ce dernier point donne une plus grande généralité à la distribution de
Boltzmann, par rapport à la distribution de Maxwell.
7.3.2 Démonstration
Soient N le
nombre total de particules et Ws la somme des énergies totales de ces particules.
Les grandeurs N et WS sont des constantes, le système étant fermé et
isolé.
Soit Wj, avec j = 1, 2 ..., m, m pouvant
tendre vers l'infini, l'ensemble des énergies possibles pour les particules. Ces energies sont soit des valeurs
discrètes, soit des intervalles W, W + dW clans le cas d'une distribution continue.
Soit Ni le nombre de particules possédant simultanément
l'énergie W1.
Le nombre Ni n'est limité que par le nombre total de particules présentes
dans le système.
On appellera configuration un ensemble complet de valeurs de Nj.
Sauf exceptions, une configuration peut être réalisée de plusieurs
façons possibles. Le tableau 7.2 montre
comment quatre particules, a, b, c, d, possédant trois
énergies possibles, peuvent être combinées pour
réaliser deux configurations données. On utilisera
l'indice i pour les configurations et l'indice j pour les énergies.
Tableau
7.2
N1= 3
N2=1
N3=0
N1= 2
<N2=0
N3= 2 abc d - ab - cd abd c - ac - bd acd b - ad - bc bcd a - bc - ad bd - ac cd - ab
La thermodynamique statistique
montre que pour N assez grand, l'occupation moyenne d'un niveau
d'énergie Wi est égale a l'occupation la plus probable de ce niveau.
Déterminer l'ensemble des Nj moyens revient donc à rechercher la
configuration pouvant être réalisée du plus grand nombre de façons
possibles.
La seule caractéristique permettant de distinguer les particules les unes des autres est leur
énergie. Une configuration i peut
donc être réalisée de ni
façons différentes
ni
= N! / (N1! N2!.... Nm!) (7.20)
Le problème revient par
conséquent a trouver l'ensemble des Ni
rendant (7.20) maximum, sous les conditions :
et
C'est un problème d'extremas liés, qui se résout par la méthode
des multiplicateurs de Lagrange.
Pour des raisons pratiques on cherchera non pas le maximum de vi,
mais celui de In v1, ce qui revient au même. Soit (13 la fonction de Lagrange. Par
définition,
où l1
et l2
sont les multiplicateurs de Lagrange. Par (7.20) it vient :
L'ensemble des N1
recherches s'obtient en résolvant le système des
équations (7.21), (7.22) et (7.25).
dF /d Nj = 0 = - d(ln Nj! - l1 + l2
Wj ) /T> d Nj (7.25)
Pour Njassez grand on peut utiliser la formule de Stirling sous la forme :
ln N! =~ N lnN -N (7.26) qui introduit dans (7.25), donne
l1
est facilement éliminé grâce à la
condition (7.21). On obtient :
Il reste a trouver la valeur de l2.
Pour cela, le recours a des arguments physiques est nécessaire.
D'après la section 7.2, l'équation (7.28) est valable dans le cas d'un gaz parfait.
Dans un espace uni-dimensionnel, l'énergie moyenne W des
particules d'un tel gaz vaut 1/2 kBT, par conséquent,
En prenant pour variable la quantité de mouvement p;
des particules au lieu de leur énergie
Wi d'une part, en remplaçant dans (7.29) la somme par une
intégrale, la distribution des vitesses des atomes d'un gaz parfait étant continue, on
obtient :
En faisant usage de (7.8.1) et (7.8.2) il vient :
l2 = 1/kBT (7.31)
On peut maintenant expliciter totalement (7.28) :
et obtenir la distribution de Boltzmann (7.32), représentée
à la figure 7.3
7.4.1 Champ d'application
La distribution de Fermi-Dirac régit le comportement d'un ensemble de particules ponctuelles de nature quantique,
Etant de nature quantique, les particules sont soumises au principe
d'exclusion de Pauli La distribution de Fermi-Dirac apparait donc
comme une distribution de Boltzmann, modifiée par la condition
supplémentaire de respect du principe de Pauli. Mais
l'incidence de cette condition est considérable et les deux distributions ne
conservent de ressemblance que dans le domaine des énergies élevées.
7.4.2 Démonstration
Soit un système
dans lequel chaque niveau d'énergie permis peut être
soit inoccupé, soit occupé par une seule particule
(ensemble non dégénéré).
Considérons deux particules de cet ensemble, possédant des énergies
initiales W1 et W2, respectivement W3 et W4après
avoir subi un choc l'une contre l'autre. Le théorème de la conservation de l'énergie impose
que
W1 + W2 = W3 + W4
= W1 - dW +
W2 + dW (7.33)
puisque les chocs sont supposés élastiques.
Le terme dW représente le transfert d'énergie d'une
particule à l'autre.
Les chances d'observer le choc décrit par (7.33) dépendent :
des probabilités que deux particules aient les énergies W1 et W2
respectivement,
des probabilités que les deux états W2
et W4 ne soient pas occupés. Dans le cas contraire, le principe de Pauli interdirait le choc.
Soit f(W) la probabilité qu'une particule
de l'ensemble possède l'énergie W. Le terme 1
- f(W) représente la probabilité que le niveau d'énergie W soit inoccupé.
Toutes les probabilités concernées étant indépendantes les unes des
autres, la fréquence v de collisions du type (7.33) vaut :
v = a f (W1) f (W2) [1 - f (W3)]
[1 - f (W4)] (7.34) où a est un coefficient de proportionnalité dépendant du nombre total de
particules et de leur nombre volumique. Le système étant en équilibre, le
principe du bilan détaillé [68] impose que la fréquence
des chocs du type (7.33) soit égale a la fréquence des
chocs inverses donnée par
v = a
f(W3) f(W4) [1 - f(W1)][1 -f(W2)] (7.35)
En comparant (7.34) et (7.35) on peut écrire,
(1 - f(W1)) / f (W1) (1 - f (W2))
/ f(W2) = (1 - >f(W3)) / f(W3 ) (1 - f(W4)) / f (W4 ) (7.36)
soit encore, en introduisant la quantité d'énergie
transférée au cours du choc dW,
(1 - f (W1 )) / f(W1 )
(1 - f(W2)) / f(W2 )
= (1 - f(W1 - d W)) / f(W1 - d W)
(1 - f(W2 + d W)) / f(W2 + d W) (7.37)
Cette équation ne peut être satisfaite que si
1 - f ( Wi
) / f ( Wi
) = C exp
( bWi) (7.38)
où
i = 1, 2, 3 ou 4; C et b
sont des constantes. Dans le cas général, i désigne
n'importe quel niveau d'énergie permis. De (7.38) on tire,
f (Wi ) = (C exp
(bWi
+ 1))-1 (7.39)
Mathématiquement,
C et b peuvent avoir des valeurs quelconques, pour autant
que f(Wi) < 1 conformément à la définition d'une probabilité. Ces deux
constantes doivent être déterminées sur la base d'arguments physiques.
Considérons une plage d'énergies
suffisamment élevées pour que la probabilité
d'occupation d'un niveau y soit très faible. En supposant que le principe de Pauli n'existe
pas, la probabilité d'occupation d'un niveau par deux particules ou davantage
y serait infinitésimale. Par conséquent la
distribution n'est pas affectée, dans cette plage, par
le fait que les particules sont soumises ou non au principe de Pauli.
En d'autres termes, la distribution de Fermi-Dirac tend, dans cette plage, vers la
distribution de Boltzmann.
Aux énergies élevées, (7.39) se réduit
f (Wi ) = C-1
exp (-
bWi
) (7.40)
En comparant cette expression avec la distribution de Boltzmann (7.32), on constate que
b = 1/kBT (7.41)
La constante C dépend de l'ensemble de particules
étudié et de leur environnement (système).
On pose, par définition de WF,
C = exp (- WF/kBT) (7.42)
La constante WF porte le nom d'énergie de Fermi. En portant (7.41) et (7.42)
dans (7.39) on obtient la distribution de Fermi-Dirac F(Wi),
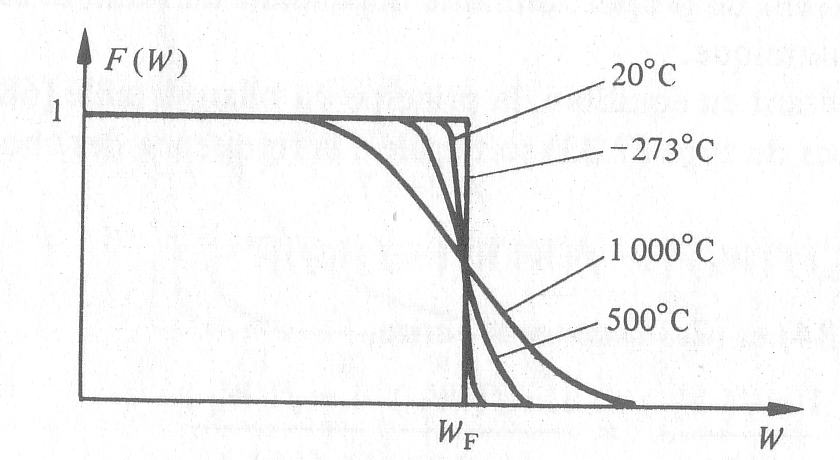
représentée à la figure 7.4 :
(7.43)
Propriétés de la distribution de Fermi-Dirac
La distribution de Fermi-Dirac dépend d'une variable indépendante, l'énergie
Wi, et de deux paramètres, l'énergie de Fermi WF et la température absolue T
L'examen de l'équation (7.43) permet de déduire les propriétés
suivantes de la distribution : F(W) = 1 pour W < WF (7.44) F(W) = 0 pour W > WF (7.45) Au zéro absolu, tous les niveaux correspondants à
des énergies inférieures à l'énergie de
Fermi sont occupés, alors que tous les niveaux correspondants à
des énergies supérieures sont vides. A une température quelconque différente de 0 K
on peut distinguer trois régions: 1) la région des basses énergies, oùw< WF.
Alors, par développement limité de (7.43), on trouve
La probabilité de non occupation d'un état vaut exp[(Wi- WF)kB
T];
2) la
région des hautes énergies, ou W > WF. Dans (7.43),
1 devient négligeable devant l'exponentielle, au dénominateur, par conséquent,
on retrouve la distribution de Boltzmann;
3) la région ou W = WF, dans laquelle se situe la transition entre les niveaux fortement
occupés et les niveaux faiblement occupés. La rapidité
de cette transition dépend de la température, (tab. 7.5).
Tableau
Taux d'occupation
Energie correspondante
unités de kBT
eV à 20°C
95 %
WF - 2,95
WF - 0,056
90 %
WF - 2,20
WF - 0,075
10 %
WF + 2,20
WF + 0,056
5.00%
WF + 2,95
WF + 0,075
(7.10)T>
(7.11)
(7.12)
>
(7.13)
(7.14)
(7.16)
(7.17)
(7.18)
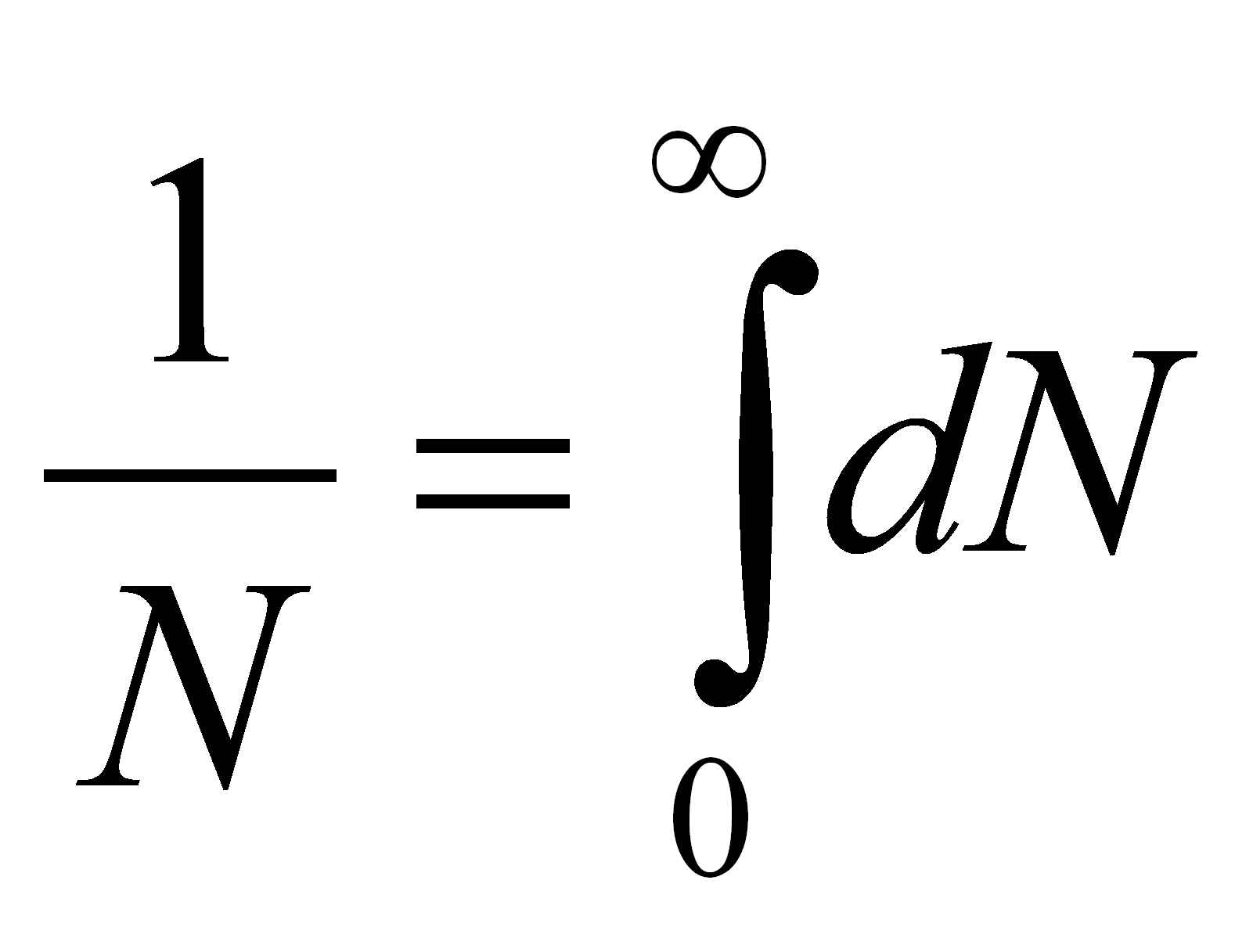(7.19)
7.3 Distribution statistique de Boltzmann
(7.21)
(7.22)
(7.23)
(7.24)
(7.27)
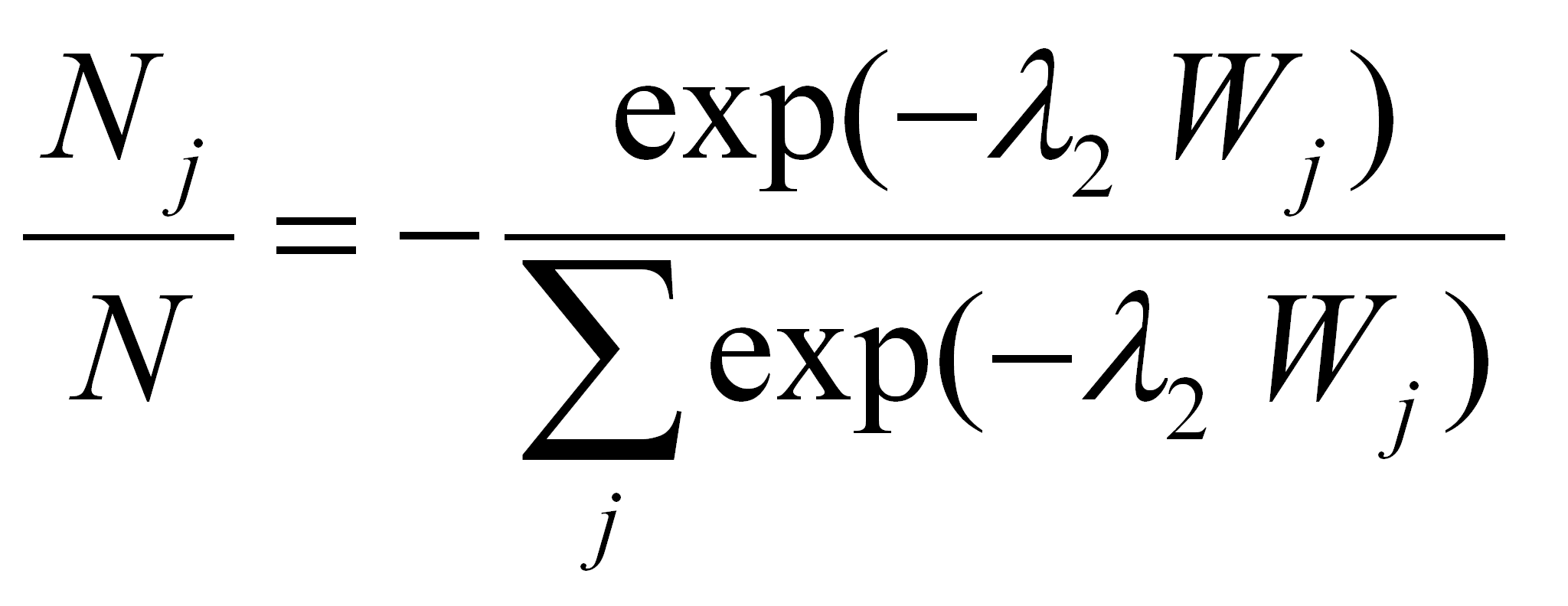(7.28)
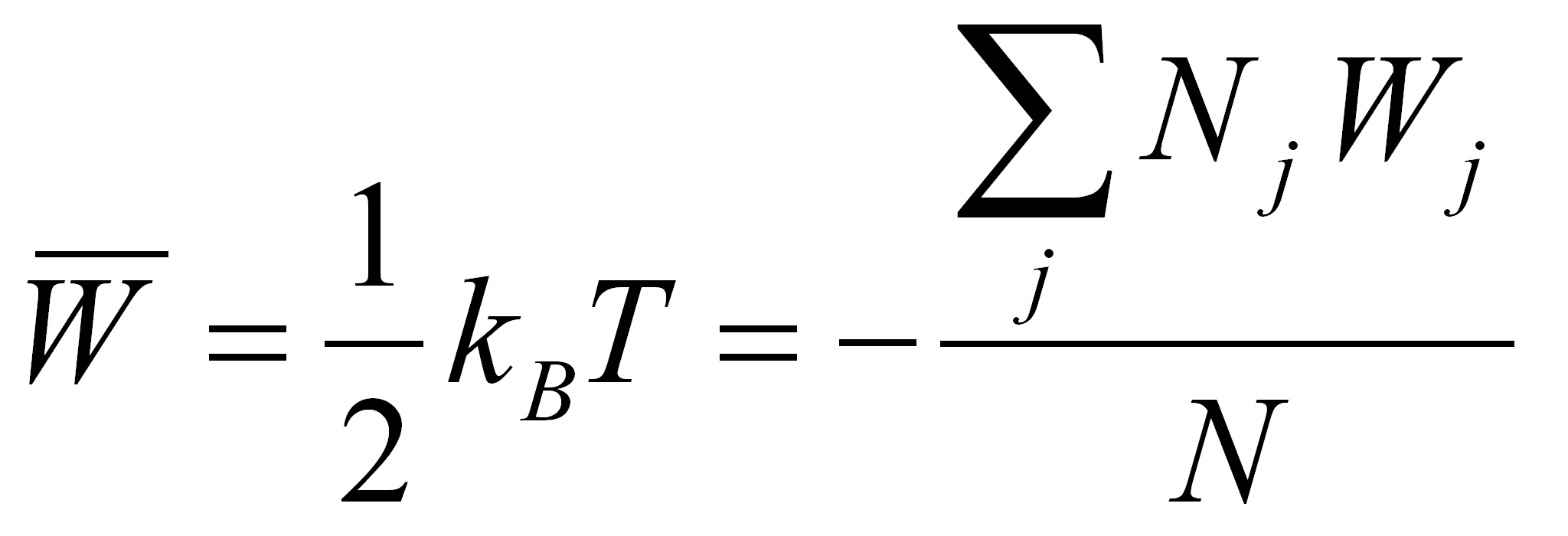(7.29)
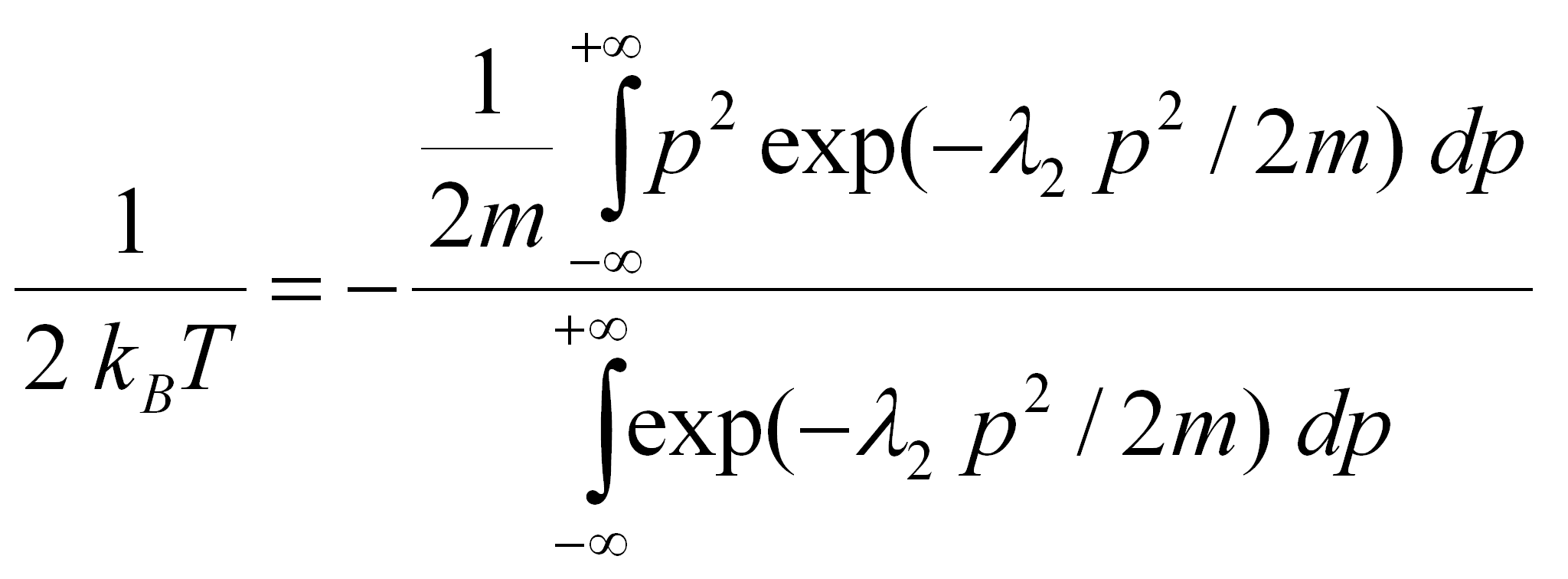(7.30)
(7.32)
7.4 Distribution statistique de Fermi-Dirac
(7.46)
(7.47)