Exercices

1.8 EXERCICES

1.8.1     Ecrire sous forme développée la fonction d'onde pour l'orbitale sphérique de l'atome hydrogène, définie par les nombres quantiques n = 2, l = 0, m = 0. Calculer les deux rayons correspondant à des maximas de probabilité de présence de l'électron.

1.8.2      On décrit l'énergie de liaison de KCl - cristal ionique par l'expression W = A^-n - Br^-m avec m = 1, n = 9 et B = 1,75 e²/4 π ε_o. Le module de compressibilité de KCl étant de 5,32 10^-11 m²/N. Calculer la distance séparant les ions K⁺ et Cl^-.

1.8.3     Calculer le facteur de remplissage atomique pour les cristaux suivants : cubique simple, cubique centré, cubique face centré, hexagonal compact.

1.8.4      Calculer le nombre d'atomes dans les plans (100) et (111) du cuivre. Ce métal cristallise en structure CFC, sa masse volumique est de 8,9 10³ kg/m³ et son poids atomique de 63,5 kg/k mole.

1.8.5     Le silicium possèdela structure cristalline du diamant. Calculer la masse volumique du silicium sachant que la longueur d'une liaison est de 0,235 nm.

1.8.6      Du zinc a diffusé dans un bloc de cuivre et, à un instant donné, le pourcentage des atomes du zinc vaut 10/(x + 0,12) où x est exprimé en cm (fig. 1.42). Calculer le nombre d'atomes de zinc traversant un plan parallèle à S, passant par x = 1 mm, puis x = 1 cm. Considérer les températures de 500C et 1 000C. L'énergie d'activation pour la diffusion du zinc dans le cuivre est de 38 000 cal/mole, d'autre part D_o = 0,033 cm²/s.

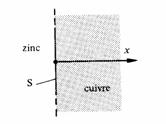
Fig. 1.42

1.8.7 Soit un milieu semi-infini, limité par un plan (fig. 1.43), et caractérisé par un coefficient de diffusion D. Trouver le nombre volumique N(x,t) satisfaisant les conditions suivantes : N(x, t = 0) = f(x) et N(x = 0, t) = 0. Considérer tout d'abord f(x) quelconque, puis f(x) égale à une constante N_o. Méthode: considérer un milieu infini et prolonger /(x) vers la gauche pour obtenir une fonction impaire (fig. 1.44)

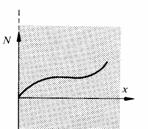
Fig. 1.43

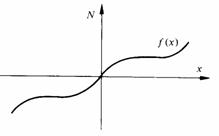
Fig. 1.44