
|
|
back
MENU
|
|
Private
|

ESR
Equivalent resistance models
The technical capacitor model shows that the impedance real part is the sum of two contributions: the capacitor series resistance serie rs and the parallel resistance rp.
The contribution due to rs becomes important at high frequency
while the contribution due to rp has a dominating effect essentially at low frequency,
in particular at the industrial frequency.
In the practical measurements, it's not possible to differentiate the 2 contributions. To overcome this problem equivalent models have been developped.
At low frequency, the Equivalent Parallel Resistance (EPR) model is used; at high frequency the Equivalent Series Resistance (ESR) model is used.
Equivalent Series Resistance (ESR)
All the dissipative composants are collected in a new resistance which is called the Equivalent Series Resistance and is specified as "ESR".
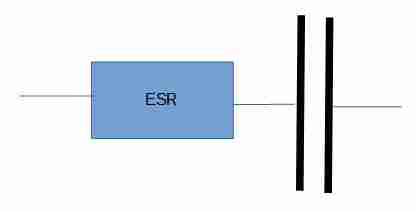
The impedance in the technical capacitor model is given by:
Z = R + j X = (rs + rp/a) + jw(L - C rp2/a) where a = 1 +(w C rp)2
The impedance in the Equivalent Series Resistance model is given by:
Z = ESR - j/wCs
Comparing both the real and imaginary part, it gives:
ESR = rs + rp/a
and
Cs= 1/w2/(C rp2/a-L)
The plot below shows a simulation of the ESR with:
C = 100 nF
L = 100 nH
rs = 10 mΩ
rp = 100 kΩ
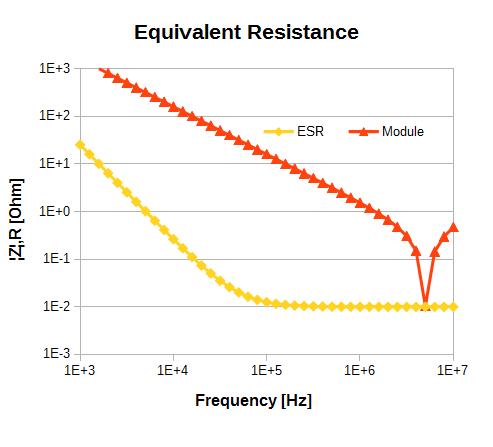
At the resonnance the impedance module is equal to the real part of the impedance.
At a given frequency the power losses are given by: PL = ESR i2.
Source: Garmanage: Roland Gallay