Derating

Weibull survivor function

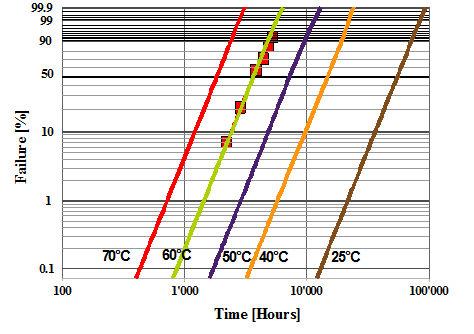
Failure mode = cell opening

Survivor = cell not opened

Voltage = 2.7 V

Temperature = 60C (green curve)

Extrapolation to

70C (red)

50C (blue)

40C (Orange)

RT (brown)

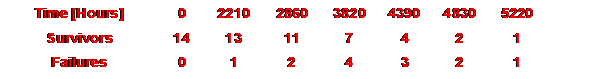
λ_o = 3900 hours

p = 5

Red square: measurment performed on a batch of 14 supercapacitors with a weak pressure release device. The failure of 1 piece represents the loss of 7,1% of the tested population.

 

Coefficient p and λ_o

The coefficient λ_o and p must be determined.

for all the failure modes

for all the operating temperature

for all the operating voltage

It is done experimentally for

Several temperature ( 40C, 50C, 65C, 70C, -.)

Several voltage (2.3 Vdc, 2.5 Vdc, 2.7 Vdc, 2.9 Vdc,

The coefficient p and λ_o for the other temperatures and voltages are calculated with the derating laws presented below.

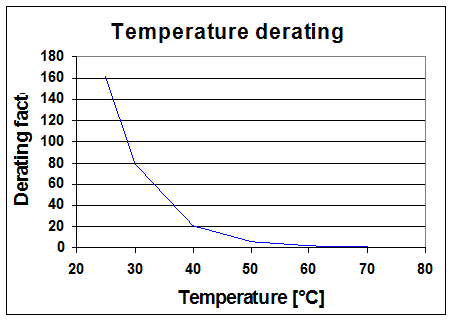
Lifetime temperature derating

Failure mode = 20% capacitance loss

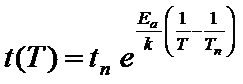
Temperature derating factor in the Arrhenius law: E_a /k = 12800 [K] which corresponds to an activation energy of 1.1 eV.

Arrhenius law

where

t(T) is the lifetime at the temperature T,

t_n is the lifetime at the reference temperature of 65 C,

E_a is the activation energy determined by the experimental data.

k is the Boltzmann constant (1.38 10²³)

T_n = 338 K is the reference temperature (65 C).

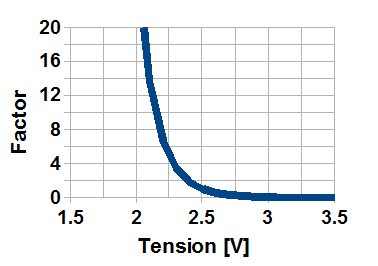
Inverse power voltage derating

Failure mode = 20% capacitance loss

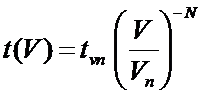
Inverse power law

where

t(V) is the capacitor lifetime with the voltage V and the reference temperature of 65 C,

t_vn is the capacitor lifetime for the reference voltage of V_n and 65 C,

N is a constant determined experimentally (15 in our example),

V_n is the reference voltage (2.5 Vdc in our example).

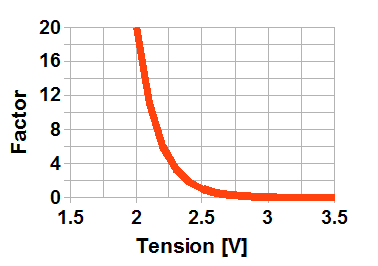
Exponential voltage derating

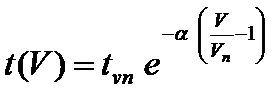
where

t(V) is the capacitor lifetime with the voltage V and the reference temperature of 65 C,

t_vn is the capacitor lifetime for the reference voltage of V_n and 65 C,

a is a constant determined experimentally (15 in our example),

V_n is the reference voltage (2.5 Vdc in our example).

Derating calculation

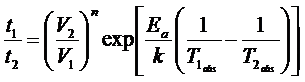
t₁ is the lifetime at the temperature T₁ and voltage V₁

t₂ is the lifetime at the temperature T₂ and voltage T₂

E_a is the activation energy determined by the experimental data

k is the Boltzmann constant

N is a constant determined experimentally.

Calculation method

The supercapacitor lifetime is determined by the failure mode which has the shortest lifetime expectancy.

(typicaly 20% capacitance loss are reached earlier than 100% of ESR increase)

From the theoretical λ_o and p obtained with the derating factors and based on the experimental data measured at 2.5 Vdc and 65C, we calculate for each temperature and each voltage the statistical time to loose 1 ^o/_oo (F(t)=0.999) of the supercapacitor of a batch.

Theoretical lifetime expectation

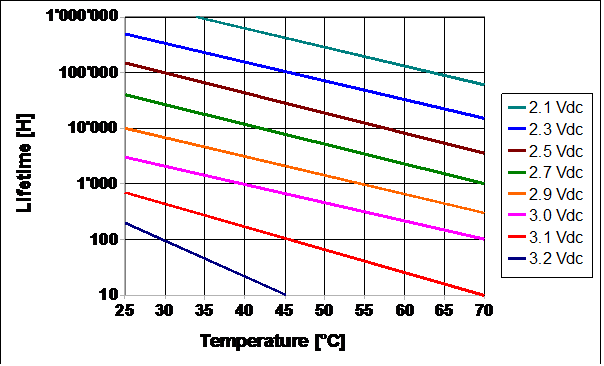
Tool for lifetime expectation calculation

Addition of all the stress ponderated contribution L(V,T) is the lifetime of the contribution at V and T.

20% capacitance drop time statistic

The capacitance drop evolution must not be confused with the statistical time distribution to reach the capacitance loss of a given amount of 20% of an ultracapacitor batch.

A rough estimation shows that the time gap between the first sample and the last sample to reach the limit is about 10 % of the time to fail. In the chart the end of life is reached between 2000 and 2200 hours for a test run on 4 samples at 65C and 2.5 Vdc.

Supposing that this failure statistic is following Weibull model, the parameters will be recovered in the following way:

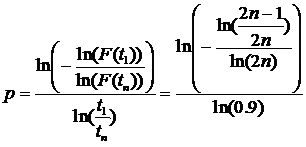
Where t_n is the time to fail for the last piece of a batch of n samples and t₁ the time to fail for the first one. 1/λ_o corresponds to the time when 36.8% (= 1/e) of survivors are remaining, or in other words, when 63.2% (= 1 1/e) of the samples have failed.

In the case of a dispersion of 10%, the accuracy is sufficient to approximate the lifetime with

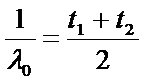
The numerical calculation shows that p = 26.

Acceleration factors based on R_p

All measurements were performed on one and the same BCAP0350 cell. After equilibrating the cell at the respective potential, the leakage current was measured 10 h after a temperature step. The logarithm of the leakage current is plotted versus the reciprocal of the temperature in K. From this type of Arrhenius plot, one could determine the activation energy of the degradation processes, provided the plots result in straight lines.

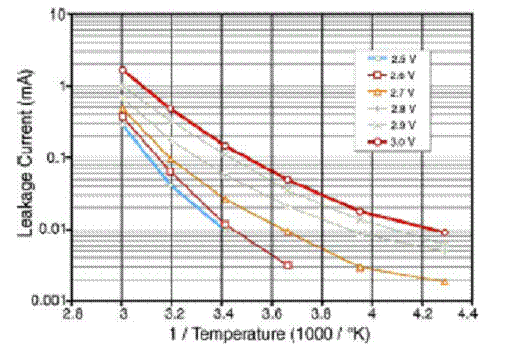
Arrhenius plot of the leakage currents at various capacitor voltages and temperatures measured after 10 h of constant conditions. At each voltage, the temperature of the EDLC was first held 100 h at 60 C before the temperature was decreased in steps of 20 C down to −40 C.

The plots do not exhibit straight lines. Only reasonable estimations for the activation energies and acceleration factors are possible. For the temperature range between 0 C and 60 C, an average activation energy of −0.57 eV (54 kJ mol−1) was determined, while in the temperature range 0 C and −40 C, the effective activation energy was only − 0.22 eV (21 kJ mol − 1). These activation energies are lower than the 0.8 eV usually assigned for Aluminum electrolytic capacitors.