Ferro

4.9 FERROÉLECTRICITÉ, PIÉZOÉLECTRICITÉ ET AUTRES PROPRIÉTÉS

4.9.1  Ferroélectricité, introduction et définitions

On appelle matériau ferroélectrique, un matériau diélectrique dans lequel les moments dipolaires sont couplés.

Ce phénomène de couplage constitue la ferroélectricité.

Le préfixe ferro a été choisi en raison des très nombreuses analogies entre ces matériaux et les matériaux ferromagnétiques.

Les matériaux ferroélectriques sont caractérisés par une permittivité relative extrêmement élevée, de l'ordre de 10³ et même 10⁴. Toutes leurs propriétés électriques sont très sensibles à la température. La ferroélectricité disparaît au-delà d'une température appelée température de Curie ferroélectrique.

4.9.2 Domaines ferroélectriques et cycle d'hystérésis

Le couplage ferroélectrique provoque, localement, un alignement des moments dipolaires les uns par rapoort aux autres.

On appelle domaine ferroélectrique, chaque région d'un seul tenant dans laquelle tous les moments dipolaires sont alignés parallèlement les uns aux autres.

Dans un échantillon homogène, à température uniforme, chaque domaine présente une polarisation spontanée P_s (Om~²) de même valeur absolue. L'orientation de P_s par contre varie d'un domaine à l'autre, de sorte que le moment dipolaire total de l'échantillon peut être nul.

Bien que les mécanismes en jeu soient de nature différente, on peut formellement comparer l'établissement des structures de domaines ferroélectriques et de domaines ferromagnétiques (sect. 3.7). Aux énergies magnétostatiques et magnétostrictives correspondent les énergies électrostatiques et electrostrictives ( 4.9.6). Les moments dipolaires présentent également des énergies d'échange et d'anisotropie.

L'application d'un champ électrique augmente l'énergie des domaines, d'autant plus que la direction de leur polarisation spontanée s'écarte davantage de celle de ce champ. Au fur et à mesure que le champ croît, la fraction en volume des domaines alignés parallèlement à E augmente donc, jusqu'à ce que l'échantillon complet ne devienne lui-même qu'un seul domaine, pour E > E_s (fig. 4.39).

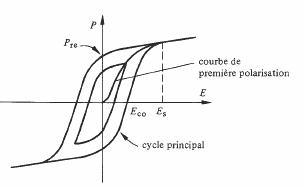
Fig. 4.39 Cycle d'hystérésis ferroélectrique.

La variation de la structure des domaines étant un phénomène irréversible, la fonction P (E) est fortement non linéaire dans la région 0 < E < E_s. Dans le cas d'un champ alternatif, P(E) prend dans cette région la forme d'un cycle d'hystérésis ferroélectrique.

Différentes grandeurs caractéristiques sont définies sur ce cycle, comme sur le diagramme B-H des matériaux ferromagnétiques. Ce sont en particulier :

•   •  la permittivité initiale, définie sur la courbe de première polarisation, par la relation :





•   •  le cycle d'hystérésis principal, qui est le cycle obtenu dans un champ alternatif d'une amplitude au moins égale à E_s ;
•   •  la polarisation rémanente P_re et le champ coercitif E_co définis par les intersections du cycle principal avec les axes

4.9.3 Polarisation spontanée en fonction de la température

L'existence potentielle de la ferroélectricité est contenue dans les expressions menant à l'équation de Clausius-Mosotti (4.56). En tirant P de (4.55), il vient :

                                      (4.185)

Dans un diélectrique ordinaire (isotrope) P et E sont parallèles, le dénominateur de (4.185) est donc positif. Si ce dénominateur décroît jusqu'à s'annuler,

                           (4.186)

une polarisation spontanée devient possible. Mais si P <> 0 alors que E = 0, l'expression du champ local (4.35) se réduit à :

                                        (4.187)

et (4.185) cesse d'être valable, (4.55) se réduisant précisément à (4.186), qui ne contient pas P. La condition d'existence d'une polarisation spontanée doit donc être écrite :

                            (4.188)

Dans un diélectrique donné, les a; sont pratiquement des constantes, sauf le facteur de polarisation par orientation a_or qui varie en fonction de la température. Séparons dans (4.188) ce facteur. Par (4.51), il vient :

                                     (4.189)

Dans cette expression S' regroupe tous les processus de polarisation présents, à l'exception de la polarisation par orientation. La température maximum 0 satisfaisant encore (4.189) est la température de Curie ferroélectrique

                     (4.190)

L'interprétation de ce résultat est en principe très simple. Le couplage produisant l'alignement des moments dipolaires ne peut se manifester que pour T < 0. Au delà de 0, il est complètement masqué par l'agitation thermique. Ici encore, l'analogie avec le ferromagnétisme est remarquable.

Dans le cas où la polarisation par orientation joue un rôle nettement prépondérant, la susceptibilité diélectrique x_r au-dessus de 0 se calcule facilement. L'équation (4.190) se réduit à

                                     (4.191)

En portant cette expression dans (4.185) il vient, compte tenu de (4.23)

                                        (4.192)

C'est la loi de Curie-Weiss (3.53), déjà rencontrée pour les matériaux ferromagnétiques.

4.9.4 Origine de la ferroélectricité

La ferroélectricité ne se rencontre que dans quelques structures cristallines particulières. D'une structure à l'autre, le mécanisme responsable du phénomène varie. Le cas du titanate de baryum BaTiO3 sera choisi à titre d'exemple, en raison de l'importance pratique de ce matériau.

Au-dessus de la température de Curie (120°C), BaTiO₃ possède la structure perovskite (fig. 4.40).

 

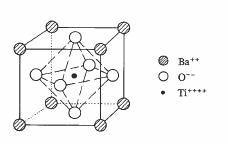
Fig. 4.40 Structure perovskite.

 

Les huit ions de baryum sont placés aux sommets d'un cube, dont les centres des faces contiennent les ions oxygène. L'ion titane occupant le centre du cube, le moment dipolaire de la structure est égal à zéro.

Au-dessous de la température de Curie, cette structure se déforme légèrement, passant de cubique à tetragonale (fig. 4.41). Les déplacements d' et d" sont de l'ordre de 10^-11 m, le côté du cube valant environ 4 10^-10 m. Ils confèrent à la structure déformée un moment dipolaire qui, par raison de symétrie, peut posséder six orientations différentes. L'interaction entre dipôles voisins provoque l'alignement responsable de l'apparition des domaines ferroélectriques.

 

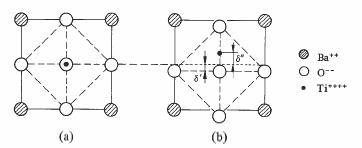
Fig. 4.41 Structure perovskite: (a) originale (T > Θ) (b) déformée (T < Θ). Projection sur un plan 1,0,0

Il est équivalent de prétendre que la structure cristalline de BaTiO₃ est simplement plus déformable qu'une autre. Une déformation locale fortuite produisant un moment dipolaire, elle crée aussi un champ local initial provoquant l'apparition d'autres moments dipolaires dans le voisinage. A leur tour, ceux-ci renforcent le champ initial, ce qui tend à augmenter encore les moments dipolaires locaux et à en créer d'autres plus loin. Cette évolution n'est finalement stoppée que par l'accroissement des forces de valence lorsque le déplacement relatif des ions augmente. Dans cette optique, la température de Curie marque l'instant où l'effet du champ local créé par la polarisation cesse d'être masqué par l'agitation thermique.

Deux autres transformations cristallines se produisent encore dans BaTiO₃. Vers 0°C la structure passe de tetragonale à monoclinique, la polarisation s'orientant selon la diagonale d'une face. Vers -80°C elle devient rhomboédrique et la polarisation s'aligne sur la grande diagonale du rhomboèdre.

 

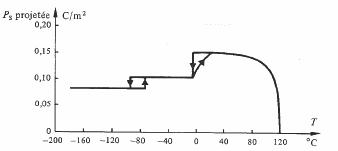
Fig. 4.42 Projection de la polarisation d'un monocristal de BaTiO₃ sur une arête du cube, en fonction de la température, d'après [61].

En tenant compte de l'angle entre l'arête du cube et la polarisation, on constate que le module de la polarisation spontanée est presque le même dans les trois structures (fig. 4.42). L'explication de la ferroélectricité par déplacements d'ions est valable non seulement pour BaTiO₃ mais encore pour d'autres matériaux, de structure perovskite ou d'une structure différente. Dans les cristaux uniaxes, tels que le sel de Rochelle (KNaC₄H₄O₆), le sulfate de triglycine (TGS) répondant à la formule (CH₂NH₂COOH)₃ -H₂SO₄ les phosphates dihydrogénés, de potassium et d'autres éléments (KDP) (KH₂PO₄), la ferroélectricité est due à une propriété de la liaison hydrogène.

4.9.5 Piézoélectricité

Certains diélectriques cristallins jouissent des propriétés réciproques suivantes :

• ils se polarisent sous Faction d'une contrainte mécanique;
en l'absence de contrainte mécanique, leurs dimensions se modifient lorsqu'ils sont polarisés par l'action d'un champ électrique extérieur.

Ces propriétés constituent la piézoélectricité et les matériaux dans lesquels elles se manifestent sont dits piézoélectriques. Le quartz SiO₂, le titanate de baryum BaTiO₃, le phosphate d'aluminium AlPO₄ sont des matériaux piézoélectriques utilisés très couramment.

 

Dans tout le domaine des contraintes utiles, la piézoélectricité est caractérisée par une relation linéaire entre la cause et l'effet, justifiant l'emploi de la théorie de l'élasticité pour décrire l'aspect mécanique du problème. Comme la ferroélectricité, la piézoélectricité est une propriété étroitement liée à la structure cristalline. L'étude des symétries de celle-ci permet en particulier de trouver les matériaux susceptibles d'être piézoélectriques. Considérons par exemple, les deux structures bidimensionnelles représentées aux figures 4.43 et 4.44.

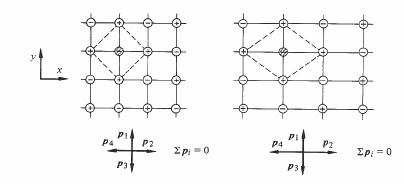
Fig. 4.43  Structure 1 : @, ion de référence.

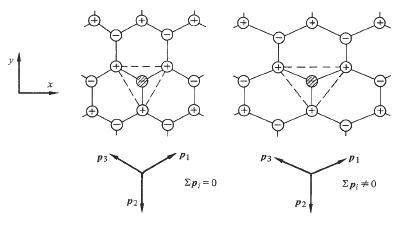
Fig. 4.44 Structure 2 : ©, ion de référence.

Il suffit, pour étudier leur polarisation, d'examiner les moments dipolaires associés aux cellules unitaires, tracées en pointillé sur les figures. On remarque que P = 0 dans les deux structures non déformées. Il en est de même dans la structure 1, déformée selon une direction quelconque du plan xy.Cela tient à ce que l'ion de référence reste le centre de symétrie de la cellule déformée.

En déformant la structure 2 par contre, l'ion de référence cesse d'être un centre de symétrie et la cellule porte un moment dipolaire résultant, d'où P différent 0. Une traction selon x (cas de la figure) fait apparaître une polarisation dirigée selon -y, et, réciproquement une compression selon x, une polarisation selon +y.

La théorie de l'élasticité [62] montre que, dans le cas le plus général, l'état de contrainte en un point A d'un solide est déterminé par 6 paramètres indépendants σ_x,σ_y,σ_z, τ_yz, τ_zx, τ_xy, constituant le tenseur des contraintes.

σ_x représente la contrainte normale [N/m²] sur un plan perpendiculaire à l'axe x, passant par A (fig. 4.45).

τ_xy représente la contrainte tangentielle [N/m²] sur le plan perpendiculaire à x et dirigée selon y. On démontre aisément que cette contrainte est égale à celle qui s'exerce sur un plan perpendiculaire à y, et dirigée selon x, faute de quoi l'élément de volume d F entourant A ne serait pas en équilibre. On a donc τ_xy = τ_yx et, au total, six contraintes indépendantes seulement au lieu des neuf auxquelles on aurait pu s'attendre. Les autres contraintes ont les significations correspondantes pour les axes y et z.

 

 

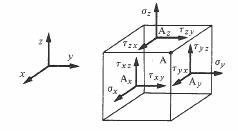
Fig. 4.45 Etat de contrainte général dans un solide. Les points A_x, A_y et A_z sont en fait confondus avec le point A. Ils n'en sont représentés distincts que pour la clarté du dessin. Dans les cristaux, le référentiel xyz est orienté selon les axes cristallins.

Sous forme générale, les composantes P_x, P_y,, P_z de la polarisation P s'expriment donc par les relations linéaires suivantes

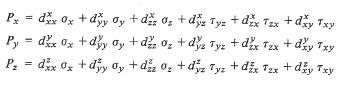                              (4.193)

On appelle les coefficients piézoélectriques. Ils s'expriment en coulomb/newton. On les écrit souvent sous la forme d'une matrice à trois lignes et six colonnes, qu'il faut multiplier par le vecteur colonne formé des contraintes σ et τ pour obtenir (4.193). Formellement, 18 coefficients sont donc nécessaires pour définir la piézoélectricité. En réalité, les symétries cristallines abaissent fortement ce nombre. Dans le cas du quartz par exemple, la matrice des se réduit à :

 

                                                             (4.194)

où

                                                     (4.195)

 

                                                    (4.196)

 

Le titanate de baryum possède trois coefficients indépendants, environ 100 fois plus élevés que ceux du quartz.

La piézoélectricité est une propriété exploitée dans de nombreux dispositifs utilisant la conversion d'une énergie électrique en énergie mécanique ou vice-versa. Citons par exemple les jauges de contraintes, certains microphones et cellules de tourne-disque, les émetteurs d'ultrasons, les lignes à retard, les dispositifs à ondes superficielles, etc.. Comme tous les corps élastiques, les cristaux piézoélectriques présentent des fréquences de résonance mécanique. En raison de la polarisation qui leur est associée, les vibrations peuvent être captées et entretenues très facilement au moyen d'un circuit amplificateur. Des étalons de fréquence très précis sont ainsi réalisés.

4.9.6 Electrostriction et pyroélectricité

Comme la piézoélectricité, Y électrostriction est une variation des dimensions d'un diélectrique sous l'action d'un champ E. Cette variation est encore liée aux déplacements de charges accompagnant la polarisation.

L'électrostriction se distingue de la piézoélectricité en ce que la déformation est proportionnelle non au champ E appliqué, mais au carré de celui-ci. C'est une propriété générale des diélectriques, se rencontrant aussi bien dans les milieux cristallins que dans les milieux amorphes, solides ou liquides. Elle ne possède pas d'effet réciproque, c'est-à-dire qu'une contrainte mécanique ne provoque pas de polarisation par électrostriction inverse. L'électrostriction est un effet pratiquement toujours négligeable.

Signalons pour terminer l'existence de la pyroélectricité, propriété de certains cristaux de modifier leur polarisation lors d'un changement de température AT. C'est un phénomène linéaire, décrit par des équations du type :

ΔΠ_i = π_i ΔT        i = x,y,z                                       (4.197)

où les π_i sont les coefficients pyroélectriques. La variation de température étant le plus souvent relativement lente, la polarisation par pyroélectricité est presque toujours masquée par un apport de charges à la surface du cristal, dû à un isolement imparfait.