Cristal

1.4   ETAT CRISTALLIN

1.4.1 Notions fondamentales, définitions

Lacaractéristique fondamentale d'un matériau dans l'état cristallin est d'être formé d'un arrangement périodique d'atomes ou de molécules.

L'étude des cristaux est l'objet d'une science, la cristallographie, qui permet, au moyen d'un langage spécifique, de décrire de façon concise les édifices cristallins les plus complexes. Seuls les éléments de cette science nécessaires pour l'étude des cristaux simples sont présentés ici.

La description d'un cristal fait appel aux notions de réseau spatial et de motif.

Dans l'espace à trois dimensions, il y a 14 façons différentes de répartir périodiquement des points, de manière que chaque point possède le même nombre de premiers voisins, situés aux mêmes distances, dans les mêmes directions. Les 14 réseaux spatiaux correspondants sont les réseaux de Bravais.

Onappelle noeud réticulaire, ou simplement noeud, chacun des points constituant un réseau de Bravais.

Le plus petit prisme dont les sommets sont occupés par des noeuds, permettant de reconstituer tout le réseau par des opérations de translation selon 3 axes de l'espace, est appelé maille, ou cellule élémentaire du réseau.

Un réseau peut être défini par ses 3 vecteurs fondamentaux a₁ , a ₂, a₃ construits sur 3 arêtes de la maille.

Dans chaque réseau, il existe une infinité de mailles différentes, possédant toutes le même volume. Parmi celles-ci on choisit généralement celle dans laquelle les modules de a₁, a ₂, a₃ sont minimum.

On passe de l'entité géométrique que représente un réseau de Bravais à un cristal réel, en limitant l'étendue du réseau à un volume fini et en associant à chaque nœud un même motif formé d'un ou plusieurs atomes ou molécules.

L'ensemble formé par le réseau de Bravais et le motif définit la structure cristalline (fig. 1.26), qui , complétée par la connaissance des vecteurs fondamentaux donne une description complète du cristal.

 

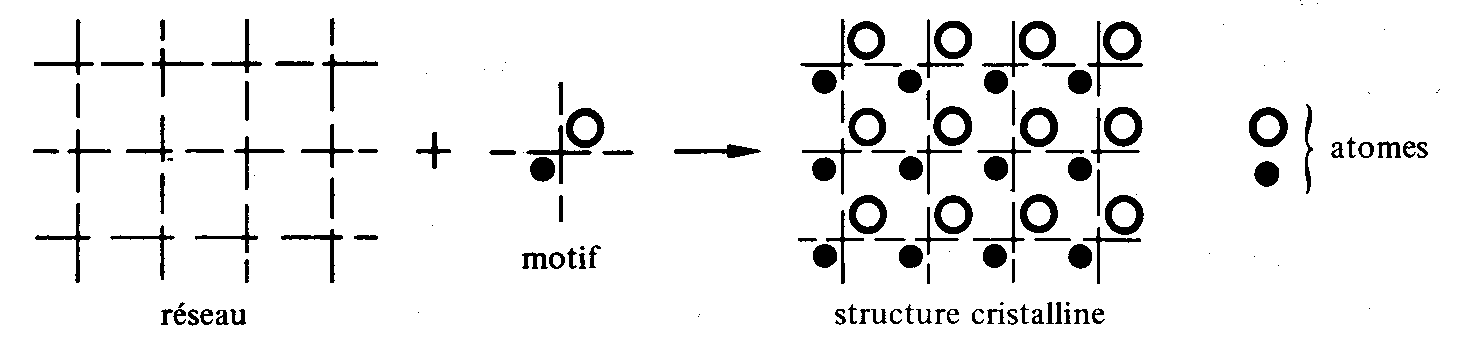
Fig. 1.26 Exemple de structure cristalline à deux dimensions.

La position du noeud par rapport au motif peut être choisie arbitrairement. Au lieu d'être placé approximativement au milieu de 2 atomes (fig. 1.26) le noeud pourrait par exemple se trouver sur l'un ou l'autre des atomes.

Par regroupement des réseaux de Bravais possédant une même maille, on définit 7 systèmes cristallins (fig. 1.27 et tab. 1.28).

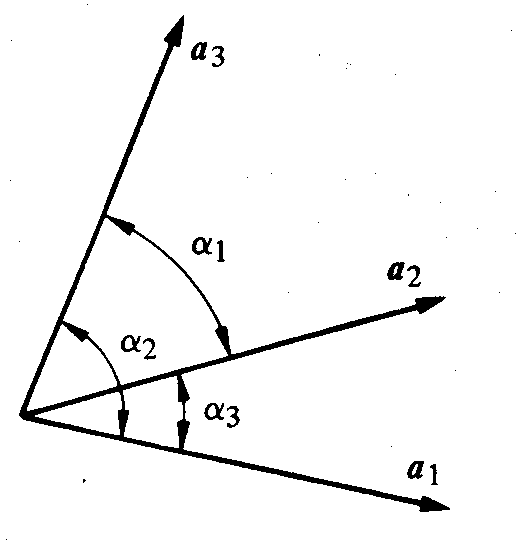
Fig. 1.27  Convention pour désigner les angles des vecteurs fondamentaux.

Un échantillon cristallin dans lequel les vecteurs fondamentaux ont la même orientation partout est appelé monocristal. Dans le cas contraire, il s'agit d'un polycristal. Un polycristal est un assemblage de monocristaux qu'on appelle plus volontiers, dans ce cas, des grains.

1.4.2 Repérage d'un point dans un cristal

La position d'un point est donnée par ses coordonnées selon trois axes x₁, x₂, x₃, prolongeant respectivement les vecteurs fondamentaux a₁, a₂, a₃. Sur chaque axe le module du vecteur fondamental est pris comme unité. Il résulte de la périodicité du cristal et de la définition de la maille que les coordonnées d'un point peuvent toujours
être ramenées à trois nombres inférieurs à 1. Dans NaCl par exemple (réseau CFC, fig. 1.15), si l'on choisit l'origine des axes sur Na, le motif est formé de Na en (0,0,0) et Cl en (1/2, 0, 0).

1.4.3 Repérage d'une direction dans un cristal

 Une direction est donnée par ses cosinus directeurs sur x₁, x₂, x_3,,  multipliés par la plus petite constante faisant de ces trois nombres des entiers. Ils sont écrits entre crochets, et surlignés s'ils sont négatifs. Un ensemble de directions équivalentes est noté entre parenthèses pointues.

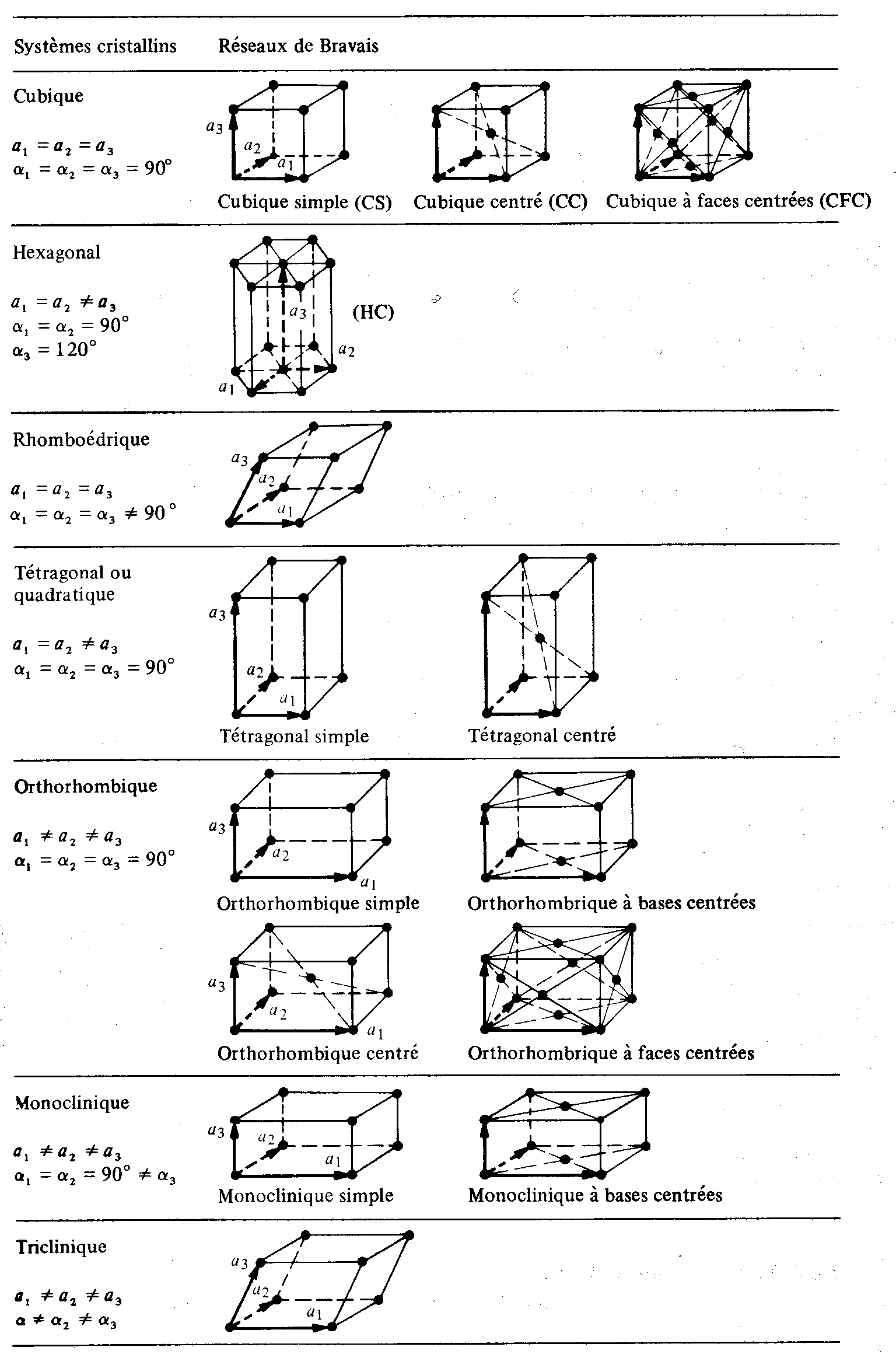
Tableau 1.28

Dans un cristal cubique simple par exemple, les directions parallèles aux axes s'écrivent [100] [010] [001] [Ï00] [0Ï0] [00Ï]. Toutes ces directions équivalentes sont désignées collectivement comme directions de la forme (100).

1.4.4 Repérage d'un plan dans un cristal, indices de Miller

L'équation d'un plan coupant x₁, x₂, x₃ aux abscisses u₁, u₂, u₃ a la forme :

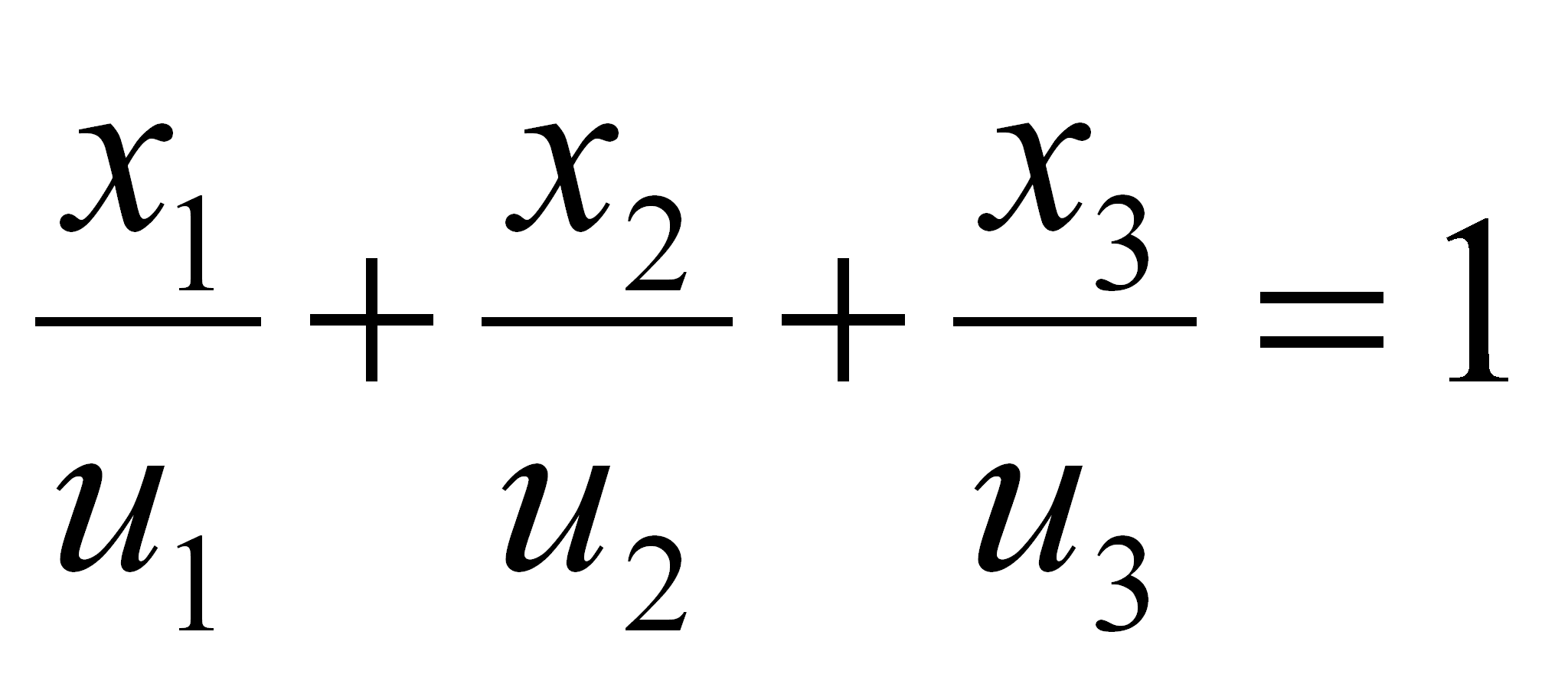(1.59)

Ce plan est décrit par les indices de Miller (h, k, l) toujours écrits entre parenthèses rondes et définis par les relations :

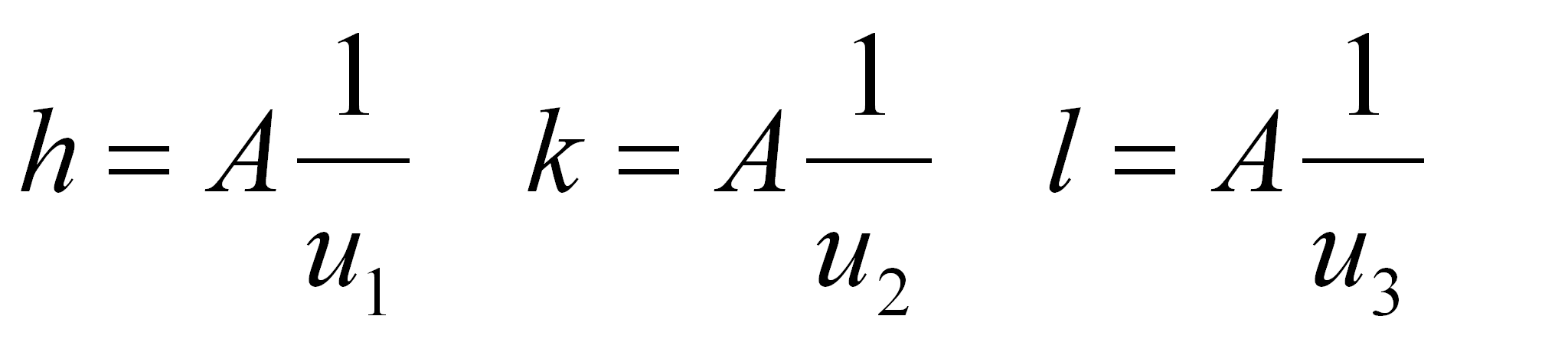(1.60)

où la constante A fait de h, k, et l, trois entiers aussi petits que possible.

Un ensemble de plans équivalents est noté entre accolades. Par exemple, les plans parallèles aux plans de coordonnées dans un système cubique simple (fig. 1.29) ont les indices de Miller (100), (010), (001), (100), (010), (001). Ils sont équivalents les uns aux autres, ce sont les plans de la forme 100.

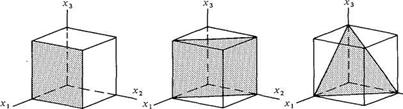
(111)

(100)                                       (110)

Fig. 1.29 Indices de Miller et plans correspondants.

1.4.5 Commentaire

La structure cristalline d'un matériau dépend avant tout des dimensions relatives des atomes et de la nature des liens de valence. Bon nombre de matériaux d'une grande importance pratique possèdent des structures cristallines relativement simples. Avant de décrire les plus courantes, il est utile de définir trois paramètres utilisés fréquemment pour les caractériser.

1.4.6 Rayon atomique. Définition

On appelle rayon atomique d'un élément, la moitié de la distance séparant le centre d'un atome du centre de son premier voisin, dans le cristal de cet élément.

1.4.7 Coordinence. Définitions

On appelle coordinence d'un atome, le nombre de ses premiers voisins.
Quand tous les atomes d'un cristal ont la même coordinence, celle-ci est appelée coordinence du cristal.

1.4.8 Facteur de remplissage atomique et modèle des sphères dures. Définitions

On appelle modèle des sphères dures la représentation schématique d'un cristal comme un empilement de sphères en contact les unes avec les autres dans certaines directions.

Dans ce modèle, le facteur de remplissage atomique est le quotient du volume des sphères compris dans la maille, par le volume de la maille elle-même.

1.4.9 Cristaux à un seul type d'atomes

Dans les cristaux où tous les atomes sont identiques, la structure ne dépend que du degré d'isotropie des orbitales par lesquelles s'établissent les liens de valence.

Lorsque ces orbitales sont sphériques, les atomes s'empilent les uns sur les autres (modèle des sphères dures) selon l'arrangement occupant le minimum de volume.
La distance entre atomes, elle aussi minimum, rend l'énergie de cohésion maximum.

Deux structures différentes, appelées structures compactes, satisfont la condition du volume minimum. Ce sont :

   •   la structure hexagonale compacte, en abrégé HC

   •   la structure cubique face centrée, en abrégé CFC

Le tableau 1.30 montre comment ces structures s'obtiennent en empilant des couches de sphères disposées de façon hexagonale.

Tableau 1.30 Structures compactes. Pour rendre ces structures bien visibles, le diamètre des sphères a été réduit sans modification de la maille.

 

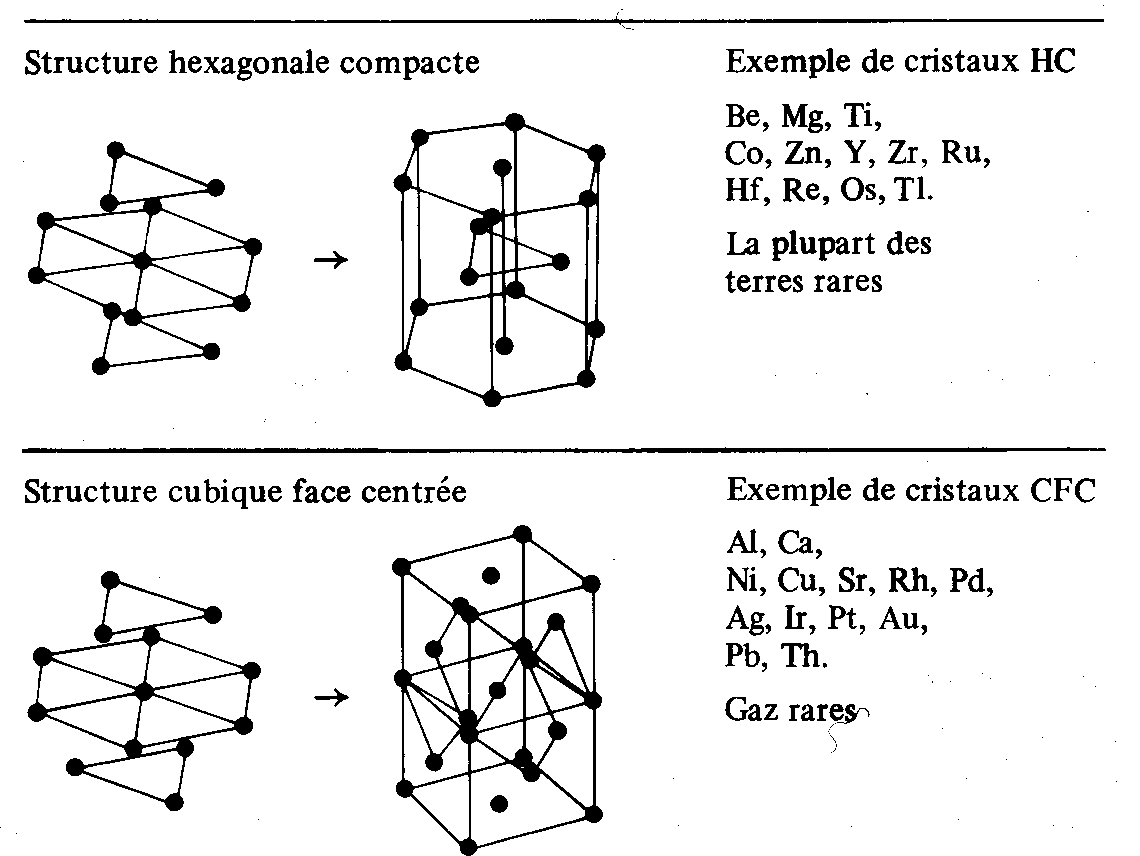
Les structures compactes possèdent la plus haute coordinence possible : 12, et le facteur de remplissage atomique le plus élevé possible : 0,740 ( 1.8.3). Trente-deux éléments métalliques possèdent, à température ambiante, une structure compacte.

Lorsque les liens de valence présentent un caractère anisotrope, la structure cubique centrée, en abrégé CC, est la plus fréquemment observée, viennent ensuite la structure du diamant (fig. 1.22 et tab. 1.31), puis les structures hexagonale, rhomboédrique et d'autres.

Tableau 1.31
Structure	Coordinence	Facteur de remplissage atomique	Exemples (20°C)
Cubique centré	8		V, Cr,Fe, Mo, W
Diamant			C, Si, Ge

La structure cubique simple, utilisée comme exemple dans de nombreux développements à caractère qualitatif est très rare. Parmi les éléments, seul le polonium la possède à température ambiante.

1.4.10 Cristaux à plusieurs types d'atomes

La diversité des structures que peuvent présenter les cristaux à plusieurs types d'atomes est très grande. Trois structures simples sont fréquentes. Ce sont :

•    •   la structure du chlorure de sodium NaCl (fig. 1.15) que possèdent également MgO, MnS, PbS, FeO pour ne citer que ces exemples.

•    •   la structure du chlorure de césium CsCl (fig. 1.15) dont le réseau de Bravais n'est pas cubique centré !  En effet, l'atome au centre du cube n'a pas les mêmes voisins qu'un atome situé dans un angle. Le réseau de Bravais de CsCl est cubique simple avec le motif Cs⁺ en (000) et Cl^- en (½,½,½). Les composés TU, Tl Br, Al Ni, BeCu entre autres ont la même structure que CsCl.

• la structure de la blende de zinc Zn S (fig. 2.44) dont le réseau est CFC avec le motif Zn en (000) et S en (¼,¼,¼). Les composés AgI, ZnSe, In As, InSb, SiC, AIP possèdent cette structure.

D'autres structures plus complexes sont décrites plus loin. La structure tungstène à propos des supraconducteurs (fig. 2.79), la structure spinelle à propos des ferrites (fig. 3.33), la structure perovskite à propos des ferroélectriques (fig. 4.40).

1.4.11 Variétés allotropiques et polymorphisme

Certains éléments peuvent se présenter sous plusieurs structures cristallines, constituant les variétés allotropiques de l'élément. Une allusion à cette propriété, appelée polymorphisme, a été faite plus haut ( 1.3.4) à propos du carbone. Certains composés chimiques sont également doués de polymorphisme, la silice par exemple, qui peut se présenter sous forme de quartz, de tridymite ou de cristobalite.