
|
|
back |
|
Private
|

Time
Capacitance and series resistance characterization in the time domain
There are different methods of determining the capacitance and the series resistance in the time domain:
either with constant current, constant power or constant load
charging/discharging conditions. The first solution is the most widely used in
the laboratories because it's the easiest and the cheapest.
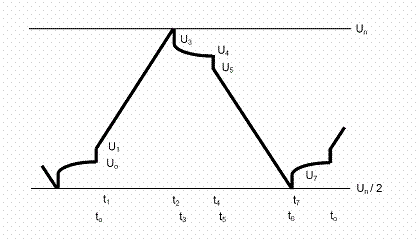
The measurement sequence starts at time to by switching on a given constant charging current. The initial instantaneous observed voltage step, from Uo to U1, is due to the current in the capacitor series resistance. The current is switched off at time t2 when the capacitor has reached the nominal voltage Un. The voltage drops instantaneously from Un to U3 due to the disappearance of the current. When the capacitor is left floating between time t3 t4, the voltage drops from U3 to U4 due to selfdischarge and charges redistribution. The constant discharging current is switched on at time t4 and switched off at time t7 when the voltage has reached half of the nominal value Un/2 or even lower values to respect particular specifications. The value of the current intensity is defined in the IEC 62391 standards and depends on the type of supercapacitor (power, backup, etc,).
The mean capacitance Cn is determined from the time necessary to discharge the capacitor between two voltage limits with a constant current I with the relation (1):
![]()
The IEC 62391 standard, which has been written to be adapted to high series resistance supercapacitor measurement, defines that the mean value should be calculated between 80% and 40% of the nominal voltage value.
The series resistance is calculated from the voltage drop which occurs at the nominal voltage between t2 and t4 during the current interruption (Eq. 2). If t4 was equal to t3 the drop would reflect exactly the value of the series resistance.
![]()
Of course this value is difficult to obtain experimentally because of the band path width limitation of the measurement apparatus. The selfdischarge due either to the leakage current or to the charge redistribution adds a contribution to the voltage drop corresponding to Rp, the parallel resistance in the model.
Source: Garmanage: Roland Gallay